
 |
|
Главная страница Приемы качественного исследования [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [ 151 ] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] цикла, не исчезающей при изменении аппроксимации, несмотря на весьма малую ее ширину (максимальная ширина порядка 0,015 для 0=1 весьма быстро убывает при о О, так как бифуркационная кривая между точками А я В касается в точке А прямой, ограничивающей снизу область 2). Грубость пространства параметров по отношению к изменению характеристики 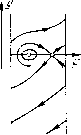 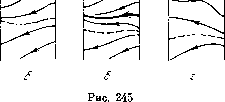 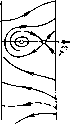 с сохранением «тонких» элементов не является очевидной и связана с сохранением для различных аппроксимаций особенностей бифуркаций при возникновении и исчезновении петли сепаратрисы. Эти особенности определяются знаком величины + Оу для седла (см. гл. 10). Для фиксированного о при возрастании параметра v можно перейти из области 1 в область 2. При этом разбиение фазового пространства, изображенное на рис. 245, а, переходит в разбиение на рис. 245, д. При значении v = vq (это значение единственное в силу монотонности изменения направления векторного поля при монотонном изменении v) а- и ш-сепаратрисы седла на нижнем полуцилиндре должны образовать петлю, охватывающую цилиндр. От петли, однако, не может появиться неустойчивый предельный цикл, изображенный на рис. 245, д, так как седловая величина, которая при обеих аппроксимациях (см. рис. 243, а, б) с точностью до членов порядка р дается выражением Рф -Ь = = -р,рог, в интервале 0<о<1 отрицательна (Р>0), и, следовательно, при возрастании v в петлю сепаратрисы должен превратиться устойчивый предельный цикл. Чтобы это оказалось возможным, необходимо должен возникнуть двойной предельный цикл при возрастании v до значения v = vo (рис. 245,б). Этот цикл затем разделяется на два (верхний - устойчивый, нижний - неустойчивый) (рис. 245, в), и устойчивый предельный цикл превращается в петлю сепаратрисы (рис. 245,г), исчезающую при дальнейшем возрастании и порождающую раз- биение, представленное на рис. 245, д (последовательные переходы от а до 5 представлены на рис. 245, а-S). Высказанные соображения позволяют выделить класс характеристик, для которых области 1 ж 2 необходимо разделяются областью с двумя циклами. Все сказанное может быть почти дословно повторено по отношению к условиям существования тонкой полосы с фазовым пространством, содержащим два предельных цикла (охватывающих состояние равновесия) и разделяющей области 2 ж 4:. При изменении характеристик, вообще говоря, будут перемещаться бифуркационные кривые на плоскости параметров и их точки пересечения. Если на плоскости параметров есть точки, в которых пересекаются более двух бифуркационных кривых (и, следовательно, смыкаются более четырех областей), то окрестность таких точек при изменении характеристик может изменить качественную структуру разбиения плоскости параметров при соответствующем изменении характеристики. Сохранение структуры разбиения плоскости параметров в этих точках требует более жестких условий для класса характеристик, не изменяющих структуру разбиения плоскости параметров. Такой точкой, например, для рассматриваемой плоскости параметров о, v при характеристиках рис. 243, а, б будет точка А, в которой смыкаются пять областей. Неизменность качественной структуры разбиения плоскости параметров системы (9) при характеристиках рис. 243, а, б обуславливается тем, что величина Рц) Л- Qy с точностью до величин порядка р для фокуса и для седла имеет одинаковое значение при обеих аппроксимациях, и при изменении знака о не только появляется цикл из особой точки, но и происходит изменение характера бифуркаций для петли сепаратрисы. Это условие не будет соблюдено, если перейти к релейным характеристикам. Рассмотрим [109] систему (9) с релейными характеристиками (см. рис. 243, в) и малым параметром р. При р = о система будет иметь интеграл [у2/2 - ф! - л < ф < о. Замкнутые кривые семейства (13) при 0</г<л охватывают особую точку, при л < ft < оо - фазовый цилиндр. Система будет иметь особые точки на линиях сшивания: в точке Oi(0, 0) - квазифокус, в точке Oz[n, 0)-седло, сшитое из обыкновенных траекторий. Функции ifii(ft), (Уь) и ъ(Ь,) для релейных характеристик имеют особенно простой вид. Приведем выражение для ifi3(ft)/P, имеющей некоторые интересные особенности: = eVi 2т[ь-{nj" + 2n(k-пУ} (14) Здесь m = га = О, если Q<h<л/4, тга = 1, га = О, если л/4 < ft < Зл/4, т = га = 1, если Зл/4 sS ft 5£ л. На рис. 246 в плоскости (ft, 1J33/P) изображены кривые (14) для различных о. При о = 0 функция i33(ft)/P для 0<ft=n/4 совпадает с отрезком оси ft и, следовательно, имеет кон-5-=-.с тинуум корней. / Переход а через нуль, соответствующий последовательности изменения качественных структур, представленной на рис. 247, будет аналогом бифуркации, соответствующей рождению неустойчивого предельного цикла из особой точки. Предельный цикл появляется из границы области, заполненной замкнутыми кривыми. При 0 = 0 сшитое состояние равновесия на линии склейки будет «центр с точностью до величин порядка р». При учете членов порядка в полосе -л/4 = ф < л/4 будут медленно закручивающиеся или медленно раскручивающиеся спирали. В этом можно убедиться, построив, например, функцию последования на ползшрямой г/ О на линии сшивания. Она будет иметь вид 2/2 = г/1 - 4 Тг/оН- -Ь (...) + ..., I/O - параметр. Функция Ip*, описывающая бифуркации в окрестности особой точки с учетом членов порядка р, может быть получена из так называемых вторых приближений. Приведем уравнения границ на плоскости (о, v): А) 0 = 0, 2) 0=1, 3) o = (l/4)(3V3-- 1)= 1,049..., 4) 2«v - (1/3) (4о + 1 - 3V 3) = О, 5) 2л\ + (1/3)Г2л32(4д + 1 зуз)=о, 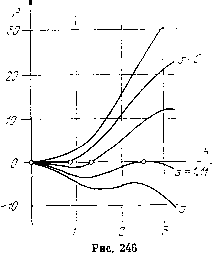 = i5 [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [ 151 ] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] 0.0138 |