„3 ( 2мф/л

- л < ф < о, = 0<Ф<л, m

для которого производная dHjdy непрерывна на линиях сшивания ф = О и ф = ±л.

Замкнутые кривые семейства (18) при -2/3</i<0 охватывают состояние равновесия типа сшитый центр, а при О < <h<°° - фазовый цилиндр. Состояния равновесия 0\ (-л/2, 0) п 02(л/2, 0) будут седла. Функция {h) здесь будет иметь вид

() = ТI ("f + 2 -У - -у) У (19)

г

а ei И 62 имеют те же значения, что и в предыдуш;ем случае.

Исследование обнаруживает тождественность поведения и свойств функций ij3(ft) для исходной и аппроксимируюш;ей систем по отношению к зависимости корней от параметра к. Со-ответствуюш;ие бифуркационные значения к для аппроксимирующей системы будут /с = 3; 9/5; 1,65. Пространство параметров системы будет отличаться от представленного на рис. 250 лишь незначительным смещением заштрихованной полосы, соответствующей системам с двумя циклами.

Тождественность разбиения фазового пространства для исходной и аппроксимирующей систем обуславливается здесь в первую очередь сохранением особенностей бифуркаций, связанных с сепаратрисами седел, так как седловая величина не изменилась при переходе к аппроксимирующей системе (для обеих систем в седле P<f + Qy = k\i).

Возвратимся к уравнениям (15), не предполагая более параметры аир малыми. Изменение числа состояний равновесия системы (15) происходит при а>1. Будем рассматривать область а<1, где число состояний равновесия не изменяется по сравнению со случаем малого р. Простейшие бифуркации, связанные с предельным циклом, могут быть найдены и сохраняют тот же характер, что и для малых значений а и р. Появление устойчивого предельного цикла из бесконечности происходит при возрастании р от нуля (это видно из уравнений (15) непосредственно, так как при изменении знака р бесконечность из устойчивой становится неустойчивой). Появление неустойчивого предельного цикла из состояния равновесия происходит из кривой

а-Зр "P+/i + P!o (20)

(соответствующая граница на рис. 250 есть касательная к кривой (20) в начале). Величина Рф + (?у = а =/ср для немалых

При р = О система будет иметь интеграл

\1 не изменяет знака и ооуславливает неизменность характера бифуркаций, связанных с сепаратрисами седел. Только для суждений о бифуркациях, связанных с двойным предельным циклом, нет полной информации. Знание других бифуркаций позволяет сделать ограниченные высказывания об области существования систем с двумя предельными циклами.

Для больших значений параметра р расположение сепаратрис седел будет таким, как на рис. 251, а (это непосредственно следует из расположения главных изоклин для достаточно больших Р). Не существует предельных циклов, охватывающих цилиндр. При малых р расположение сепаратрис будет, как на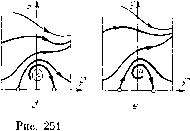

рис. 251, е (при р = 0 а-сепаратриса седла идет в бесконечность; при малых р появляется устойчивый предельный цикл из бесконечности). При убывании р векторное поле поворачивается монотонно, поэтому существует единственное при любом фиксированном ао значение Ро, при котором а- и со-сепаратрисы седел образуют петлю. Множество точек «о, Ро образует непрерывную кривую, пересекающую полосу О < а < 1.

От петли, однако, не может появиться устойчивый предельный цикл, охватывающий цилиндр, так как в седле P<t + Qy== = а> 0.

Из петли может появиться или к ней стянуться лишь неустойчивый предельный цикл; чтобы это оказалось возможным при убывании р до значения р = Ро, из сгущения траекторий необходимо должен возникнуть двойной предельный цикл, охватывающий цилиндр (рис. 251,6).

Этот предельный цикл затем разделяется на два (верхний - устойчивый, нижний - неустойчивый) (рис. 251, в), и неустойчивый предельный цикл может превратиться в петлю сепаратрисы (рис. 251,г), исчезающую при дальнейшем убывании и порождающую неустойчивый предельный цикл, который охватывает состояние равновесия (рис. 251,5). При значении р, удовлетворяющем условию (20), неустойчивый предельный цикл стягивается к состоянию равновесия и исчезает.

Описание изменений качественной структуры разбиения фазового пространства на траектории при изменении р позволяет утверждать необходимость появления области с фазовым пространством, содержащим два предельных цикла, которые охватывают цилиндр, и позволяет проследить такую же последовательность бифуркаций в зависимости от , как и для случая малого \х. Однако последовательность структур разбиения фазового пространства на траектории, представленная на рис. 251 и строго доказанная для случая малого р, может быть отождествлена с соответствующими структурами, относящимися к случаю немалого р, лишь с точностью до четного числа предельных циклов.

Логическая возможноть такого расхождения остается неустраненной, и грубость пространства параметров здесь нужно понимать в том ограниченном смысле, о котором было сказано вначале. В этом смысле приведенное описание доказывает грубость пространства параметров по отношению к переходу от малых р к немалым в довольно широкой полосе О < а < 1 пространства параметров а, .