
 |
|
Главная страница Приемы качественного исследования [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [ 30 ] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] к состоянию равновесия, нет траекторий, стремящихся в этом направлении, а все траектории в достаточно малой окрестности являются спиралями или замкнутыми траекториями. § 3. Примеры. Пример 1. dxIdt = Хх", dy/dt = by. Разделив одно уравнение на другое, получим dy/dx = by/{Kx). Это уравнение элементарно интегрируется: Пусть для определенности ЬД > 0; тогда, очевидно, если х +0, то 1/ О, а при х --О у -> +оо. Состояние равновесия - седло-узел. Узловая область расположена как на рис. 51, б, если Ь > О, Я > 0. Нетрудно также установить расположение узловой области и направление на траекториях при других знаках Ь и Я. Пример 2. д: - /-j-2/-Ь .г dx Для точки 0(0, 0): "ЗхСО.О) ?;(0,0) 2х -- X - 3* = 0, б = р;(о,о) + (?;(о,о) = 2. Подстановкой х=2у,у = --х + у преобразуем уравнение к виду У + Jx, у) dx (х, у) Ищем решение уравнения у + Q(x, y)=~y + y-j в виде ряда по степеням х. Получим г1)(х) = Л(,ф(1)) = -Р+ ... Здесь m = 3, Дш = 1/64 > О и, следовательно, точка 0(0,0) - узел. Интегрируя, получаем = + С. Нетрудно видеть, что разбиение на траектории имеет вид, представленный на рис. 53. Пример 4. dy г -I- г* - Зху -Г =-?-I-Г-» Р - целое число. хуР + у* + х Для точки 0(0, 0): А = = 0 иб = 0. Подстановкой X = -у, у = -х уравнение приводим к виду dy <?2 ) - х* - dx у+Р{х,у) у + у*-ЗхР Ищем рещение уравнения у + у* - Зху = О в виде ряда по степеням X. Находим у = ф(ж) = 0. Поэтому Mp(x) = Q2{x, <р{х))=-х\ а{х, <р{х)) = х. Здесь к = 2т = 4, п = р, а = -1, 6„ = 1. Если р<т = 2, то точка 0(0, 0) - седло-узел (это может быть только в случае р = I). Если р> т = 2, то точка 0(0, 0)- вырожденная особая точка (для нее с = 2, N = О, Nf = 0). Если в исходном уравнении будет отсутствовать член ху, то а{х, <р(а;))=0, и тогда 6„ = О и, следовательно, точка 0(0, 0) будет вырожденной особой точкой. Пример 5. dy аху-х + у 2 у) „ . 1- y + x + ixV-y - У + Р,(х,У) «1- Из уравнения у + Р2{х, у) = О находим у ==ц>{х)= -х + ..., и, следовательно, 1,(а;)= (32(а:, ц>(х))= ах(-х + .. .)-х+{-х -f .. .)2 = = -х + ... (так как п > 1), о (х, ф (х)) = Р* (ж, ф (ж)) + Qly {х, ф (а;)) = аж" + 7а;* -1- ... Таким образом, возможны случаи? 1. /г 6. Тогда 6„ = а -f 7 (/г = 6) или 6„ = 7 (/г > 6) и, следовательно, ЬпФО и п>т. Особая точка 0(0, 0) является фокусом или центром. 2. п<6. Тогда 6„ = а50 и V = Ч-4 (m-f l)aa„+i=o2-16. Теперь если /г = 4 или /г = 5, или /г = 3 и if = - 16 < О, то точка 0(0, 0)- фокус или центр. Если п = 2, то точка 0(0, 0) - узел. Если п = 3 и " = 0 -16>0, то точка 0(0, 0) -точка с замкнутой узловой областью. Пример 3. Примеры более сложных состояний равновесия. Мы предоставляем читателю рассмотреть приведенные ни- ..... У\ 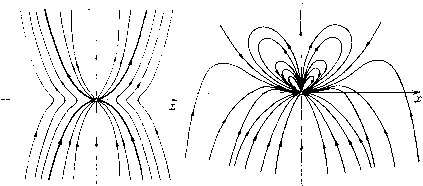 Рис. 56 Рис. 57 же примеры (во всех этих примерах системы могут быть проинтегрированы в квадратурах). Пример 6. dxjdt = ху, dy/dt = х + у. Система интегрируется путем замены у/х = и. Можно показать, что в окрестности состояния равновесия траектории имеют характер, представленный на рис. 56. Пример 7. dx/dt = ху, dy/dt = 1/2 - бху + X*. Система интегрируется с помощью замены у/х = и. Рассматривая полученный интеграл, нетрудно убедиться, что состояние равновесия имеет вид, представленный на рис. 57. Пример 8. dx/dt = ху, dy/dt = у - х\ Рис. 58 Траекториями этой системы являются кривые i/ + а;* = Сх и, кроме того, полуоси х = Q, у> Q и а; = 0, у <Q. Состояние равновесия имеет вид, представленный на рис. 58. В настоящее время методы исследования сложных особых точек получили дальнейшее развитие (список дополнительной литературы [31, 15, 17, 27]), 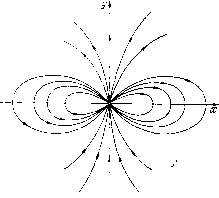 [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [ 30 ] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] 0.0089 |