
 |
|
Главная страница Приемы качественного исследования [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [ 147 ] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] И полупрямой Я, = ц для ц > (л/2)ф7. Вдоль граничной кривой характер сшитой сложной особой точки и качественные структуры разбиения на траектории будут изменяться. Если фо невелико, то сложная особая точка Оз4(фо, (Я, - 1)/ц) на интервале О <ц<(л/2)ф7 сшивается из седла О4 и фокуса или узла Оз. Для [1>(л/2)ф7 сложная особая точка Оз4(0, 1) , будет седло-узлом. Для фо, удовлет- 1- I воряюш;их условию 1 + я-<1/(2фо), я; / I граничная точка X = Я*, разделяю- --±*- щая седло-узлы и седло-фокусы, ле- жит в интервале 1 + л" < Я* < < (л/2)ф Рис. 237 Если 1 < Я< Я* и, следовательно, точка Оз4(фо, (Я--седло-фокус, то а-сепаратриса седла 0\ не может идти в особую точку и должна накручиваться на устойчивый предельный цикл, охватываюш;ий цилиндр (бесконечность неустойчива). Качественная картина эквивалентна представленной на рис. 168, - /. Для больших \1 = % м-сепаратриса седло-узла Оз4(0, 1) имеет всюду отрицательный наклон. Предельных циклов нет. Качественная картина эквивалентна представленной на рис. 168, V. При возрастании параметра ц вдоль граничной кривой осуществляются все релятивно-грубые и бифуркационные структуры, представленные на рис. 168 от - / до V. 3. Разбиение пространства параметров на области с различными качественными структурами фазового пространства. Фокус Оз(ф*, р*) всегда устойчив, если он расположен слева от оси ф = 0 (Я<р,), и может менять устойчивость, если расположен справа (р, < Я<(1 - 2л-фо)М+ !)• Если ф* > О, то Оз = (р; + (?;)з = А 2Я - 4цр* = - 2№* = 2 [2фдЯXi - (2фо -Ь я) fi -Ь я] - я(я-2фцi) - я-2ф„i Р я-2фi• Фокус меняет устойчивость на кривой, начинающейся в точке (Я = 1, ц = л [л -(2я -2)фо]-), и заканчивается на граничной кривой в точке, гдеЯ = 1-Ь я". При переходе через кривую Оз = О в направлении возрастающих \i фокус из неустойчивого становится устойчивым. Обращение в нуль седловой величины происходит на прямой Я = 1 + я~, смыкающейся с линией, на которой фокус Оз меняет устойчивость, в точке пересечения с граничной кривой К={1 ~ 2л-щ) р + 1. Отправляясь от известных структур разбиения фазового пространства на граничной кривой (структуры рис. 168 от II-III до F) и в области Я-р+1<0 (структура рис. 169, S), можно проследить все бифуркации и смены структур при монотонном повороте поля с возрастанием р. Качественная структура разбиения пространства параметров (рис. 238) не отличается от структуры разбиения исходной системы (2) (см. рис. 167). Структуры, соответствующие внутренним точкам областей разбиения пространства параметров, эквивалентны структурам в областях разбиения для системы (2). Для системы с аппроксимацией (6) возникает одна особая бифуркация. Точкам кривой оз = О на полосе О < ф < фо соответствует особая точка типа центр в точке Оз. При возрастании р и Рис. 238 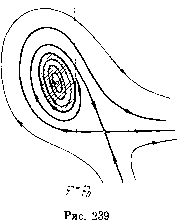 перемене знака величины Оз неустойчивый предельный цикл появляется из границы области, заполненной замкнутыми кривыми. Точкам кривой оз = О соответствует разбиение в окрестности состояний равновесия Оз и О4, представленное на рис. 239. Замечание. Область замкнутых кривых в окрестности точки Оз не может иметь своей границей сшитую петлю сепаратрисы седла О4, так как седловая величина в седле отлична от нуля. В возможности осуществления структуры разбиения, представленной на рис. 239, проявляется неаналитичность правых частей системы при аппроксимации (6). Если фо не мало, то при аппроксимациях (6) изменением параметра фо можно изменить поведение величин 03 и 04 таким 29» образом, что исчезнут условия, делавшие неизбежным появление областей суш;ествования двух предельных циклов, охватываюш;их цилиндр. При возрастании фо до значения фо = л/2 в пространстве (р, > О, Х>1) исчезает область, в которой возникновение петли сепаратрисы происходит при положительном значении седловой величины 04. При фо > л(л-Ь 1)-72 кривая Оз = О будет состоять из куска гиперболы 2фолХр, - (2фо + л)ц + п = 0 между прямой Х = 1 и точкой 1 =р,=(я/2)ф7на изломе граничной кривой. Кривая 04 = О будет состоять из куска этой же гиперболы в интервале {л/2)ц) <; Я < 1 + (седло Oi - в интервале О < ф < фо) и примыкаюш;ей к нему полупрямой К=1 + л~\ ifA >(л - 2фо)- (седло - в интервале фо < ф < л/2). При фо л/2 граничная кривая переходит в ломаную % = I (0<р,<1), X = р, (ц>1); кривая Оз = О уходит за границу рассматриваемой области X > 1, а кривая 04 = О превраш;ается в ветвь гиперболы пХц - лц-ц+1 = 0 и, следовательно, совпадает с кривой 04 = 0, полученной при аппроксимациях (3). Разбиение пространства параметров будет качественно эквивалентно разбиению при аппроксимациях (3) (см. рис. 231). § 4. Исследование роли анпроксимациЁ для уравнения маятникового типа. Уравнение (p + h(f + F(<f)=-{ (1) представляет интерес для ряда задач механики, электротехники, теории фазовой автоподстройки частоты и т. д. при различных характеристиках F{(p). Мы покажем, что если функция /(ф) дифференцируемая, периодическая с периодом 2л, кусочно-монотонная с двумя экстремумами на периоде (exstr/(a;) = 1) и такая, что /?(ф)йф = 0, (2) то пространство параметров >0, А > О будет грубым по отношению к классу характеристик F{(p). Пространство параметров разбивается на трп области, соот-ветствуюш;ие трем возможным грубым разбиениям на траектории фазового пространства (ф, ф). Различным (ф) соответствует [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [ 147 ] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] 0.0132 |
||||||||||||