ГЛАВА 10

БИФУРКАЦИИ ПРИ ИЗМЕНЕНИИ ПРАВЫХ ЧАСТЕЙ ДИНАМИЧЕСКОЙ СИСТЕМЫ

§ 1. Определение бифуркации. Бифуркацией динамической системы мы будем называть изменение качественной (топологической) структуры разбиения на траектории, происходящее при переходе от данной негрубой системы

dxldt = P{x, у), dyldt = Q[x,y) (А)

к сколь угодно близкой измененной системе

dx/dt = Р{х, у) = Р{х, у) + р{х, у),

dyldt = Q{x, y)Q{x, y)+qix, у),

имеющей качественную структуру, отличную от качественной структуры системы (а). При этом под измененными системами, близкими к системе (а), будем (см. § 8 гл. 8) понимать систему, у которых не только сами правые части Р{х, у) и Q{x, у) соответственно близки к Р{х, у) и Q{x, у), но и частные производные от Р{х, у) и Q{x, у) до некоторого определенного (каждый раз устанавливаемого) порядка близки.

у всякой негрубой системы (а) непременно существует по крайней мере одна негрубая особая траектория, т. е. либо негрубое состояние равновесия, либо негрубый предельный цикл, либо негрубая сепаратриса состояния равновесия.

Рассматривая изменение качественного характера траекторий в некоторой достаточно малой окрестности какой-либо негрубой особой траектории (т. е. в окрестности особой точки, в окрестности замкнутой траектории, в окрестности сепаратрисы или некоторого контура, составленного из сепаратрис), мы будем говорить, что рассматривается бифуркация негрубой особой траектории (или контура, составленного из особых траекторий) того или другого типа.

Простейшей бифуркацией называется бифуркация при переходе от данной системы (А), являющейся системой первой степени негрубости, к сколь угодно близким грубым системам. При рассмотрении простейших бифуркаций системой (А), близкой к системе (А), мы будем, так же как и в гл. 9, считать систему, У которой правые части Р(х, у) ж Q{x, у) и их производные до 11*

) Кроме весьма простых необходимых условий грубости состояний равновесия гамильтоновых систем для них существуют еще также условия грубости сепаратрис, которые мы здесь не приводим.

третьего порядка близки соответствеппо к Р{х, у), Q{x, у) и производным от них до третьего порядка.

Как мы видели, в случае, когда система (А) является системой первой степени негрубостп, у нее имеется негрубая (независимая) траекторпя одного пз следующих типов:

а) двукратное состояние равновесия седло-узел;

б) сложный фокус первого порядка;

в) двойной предельный цикл;

г) сепаратриса, идущая пз одного седла в другое, или сепаратриса, идущая из седла в то же седло (образующая петлю), в случае, когда в этом седле 0{х, у)

Рх {Хо,Уо) + 0у{Хо,Уо)фО.

Мы рассмотрим каждую пз этих негрубых траекторий и их бифуркации.

Мы уже говорили, что (см. § 8 гл. 8) Пуанкаре фактически пользовался понятием грубости двумерных консервативных систем (в классе консервативных систем) и рассматривал изменение качественной структуры таких систем ири изменении параметра). Им же введены термины «бифуркация», «бифуркационное значенпе параметра», которые использовались впоследствии в [2, 3] (и в настоящей книге) в более широком смысле.

§ 2. Бифуркации систем первой степени негрубости.

I. Бифуркации двукратного состояния равновесия седло-узел.

В этом случае линейной заменой переменных (на основании изложенного в гл. 4; случай А = О, о =5 0) систему можно привести к виду

dx/dt=P2{x, y) + Pz{x, У) + ...=Р{Х, у),

dy/dt = by + Q2{x, y) + ... = Q{x, у), где Pk{x, у)-однородные многочлены степени к. При этом Рх (О, 0) + Qy (О, 0) = Ь О, Р,{1,0) = уфО.

В зависимости от знаков величин Ь и f мы получаем различные случаи расположения узловой области и ее устохгаивости (см. гл. 4).

Прп достаточно малых изменениях правых частей (напомним, что мы рассматриваем только такие достаточно малые изменения правых частей, прп которых пх частные производные до третьего порядка достаточно мало меняются), при которых система делается грубой, возможны два случая:

1) либо седло-узел (рис. 99, а) разделяется на два грубых состояния равновесия - седло и узел (узел устойчив, если Ь = Р;(0, 0) + (?(0, 0)<0, и неустойчив, если Ь = р;(0, 0) +

+ Qy (О, 0) > О (рис. 99, б при условии Ь < О, Y > 0));

2) либо седло-узел исчезает (рис. 99, б).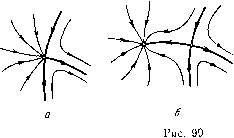

Точнее: если О - двукратное состояние равновесия типа седло-узел, то:

а) существуют ео > О и бо > О такие, что всякая систелха (А), бо-близ-кая (в к системе (А), либо не имеет в 8о-окрестности О ни одного состояния равновесия, либо имеет одно состояние равновесия типа седло-узел, либо имеет два грубых состояния равновесия, из которых одно - седло, а другое - узел, и больше никаких особых траекторий, целиком лежащих в бо-окрестности О;

б) при всяком 8 < 8о существует такое б < бо, что у всякой б-близкой к (А) системы (А), у которой в ео-окрестиости О существуют состояния равновесия, эти состояния равновесия лежат в 8-окрестностц О.

II. Бифуркации сложного фокуса первого порядка, т. е. состояния равновесия О с чисто мнимыми характеристическими корнями (-1 = ib, 2 = - ib) Tl с не равной нулю первой ляпунов-ской величиной («д =Li=f=0). Как было указано (см. § 5 гл. 3), в случае состояния равновесия с чисто мнимыми корнями все полупрямые с концом в точке О не имеют контактов с траекториями в достаточно малой окрестности О, и на достаточно близкой к О части (с концом в О) любой из таких полупрямых может быть построена функция последования, которая в рассматриваемом случае имеет вид

Р = Ро + «зРо + • • • Коэффициент аз (в других принятых обозначениях L\) и есть первая ляпуновская величина. В зависимости от знаков величин Ь О и Li О сложный фокус может быть разной устойчивости и по-разному закручиваться (см. рис. 48, 49). При достаточно малых изменениях правых частей, при которых система делается грубой (т. е. действительные части характеристических корней делаются не равными нулю):