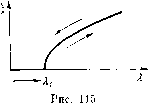) Прн всяком фиксированном Я > Я1 имеет место мягкий режим.

ллется бифуркационным; при этом значении фокус делается сложным (см. рис. 112, й).

При Я. > Я.1 из этой особой точки рождается устойчивый предельный цикл, а состояние равновесия О делается неустойчивым. Изображающая точка начинает стремиться к этому предельному циклу, так как теперь состояние равновесия неустойчиво. На физическом языке это означает, что начались колебания - имеет место самовозбуждение). При дальнейшем увеличении Я радиус предельного цикла увеличивается, а при уменьшении Я - уменьшается и при приближении Я к Я] предельный цикл сжимается в точку (в сложный фокус): колебания исчезают. На физической диаграмме (, Я) (рис. 115) имеет место плавный (мягкий) переход с постепенно меняющейся амплитудой ог состояния равновесия к периодическим движениям и обратно. Явление ведет себя обратимо.

Прибор, измеряющий амплитуду колебаний генератора при изменении параметра, покажет плавный (мягкий) переход с постепенно (без скачков) меняющейся амплитудой от состояния покоя к стационарным колебаниям и обратно.

Перейдем теперь к описанию жесткого возбуждения колебаний. В этом случае и реальная система, и соответствующие ей дифференциальные уравнения по-другому зависят от параметра, но при значениях Я < Яо (Яо - некоторое определенное значение), так же как и в рассмотренном случае мягкого возбуждения, у системы дифференциальных уравнений существует устойчивый фокус О, и изображающая точка, находящаяся вблизи состояния равновесия, будет все время находиться вблизи него (так как траектории стремятся к состоянию равновесия О при t + °о). При Я = Яо у системы из уплотнения траекторий появляется двукратный предельный цикл, который затем при Я > Яо (но Я<Я1) разделяется на два предельных цикла (рис. ИЗ, й), из которых один устойчивый. Однако это не касается изображающей точки, если она находится достаточно близко к состоянию равновесия, так как устойчивый характер состояния равновесия не меняется.

При увеличении Я устойчивый предельный цикл расширяется, а неустойчивый сжимается и, наконец, при некотором Я = Я] «влипает» в состояние равновесия О, которое делается сложным неустойчивым фокусом, а затем при Я > Я] - грубым неустойчивым фокусом. Изображающая точка (которая до Я = Я1 все время находилась вблизи точки О) «срывается» при переходе через значение Я = Я1 п «перескакивает», как ей велят траек-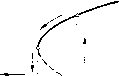

* I разному при увеличении и уменьше-

" НИИ я. Мы имеем дело с процессом,

Рис. 116 имеющим необратимый, гистерези-

сный характер (рис. И6). Это интересное для радиотехники (а также для других областей науки) явление жесткого возбуждения колебаний получает здесь на языке состояний равновесия, предельных циклов и бифуркационных значений параметра естественное адекватное объяснение. Значения параметра Я1 и Яо, соответствующие сложному фокусу и двукратному предельному циклу, являются, очевидно, бифуркационными*).

Понятия мягкого и жесткого режимов, мягкого и жесткого возникновения колебаний введены при рассмотрении лампового генератора, когда фазовая плоскость имеет весьма простой вид: при всех значениях параметра существует только одно состояние равновесия - фокус и в зависимости от значений параметра могут существовать окружающие его предельные циклы.

*) Из рассмотренной картины, например, сразу видно, что при значениях Яо < Я < Xl изображающую точку можно «перекинуть» из одного устойчивого режима в другой достаточно сильным толчком.

тории, И, следовательно, приходит к устойчивому предельному циклу (амплитуда которого все время возрастала, начиная с Ко) (см. рис. ИЗ, б). Будем теперь уменьшать Я от значения Я > Я.1 до Я, < Яо. Изображающая точка будет при всех Я > Яо все время оставаться вблизи устойчивого предельного цикла L2 (грубо говоря, двигаться по этому циклу) до тех пор, пока при Я = Яо с ним не сольется неустойчивый предельный цикл, образуя двукратный цикл, который затем при Я < Яо исчезает. После этого изображающая точка вынуждена будет «перескочить» к состоянию равновесия О, которое теперь устойчиво. Изображающая точка не будет реагировать на то, что при Я = Ki состояние равновесия делается устойчивым (из него рождается тот неустойчивый предельный цикл, который затем сливается с устойчивым), так как это не меняет характера того предельного цикла, по которому она при этом значении движется. При переходе же через значение Я=Яо (при котором цикл Li, сливаясь с циклом L2, делается двойным и затем исчезает) изображающая точка, следуя траекториям, перейдет к состоянию равновесия

и останется там при дальнейщем уменьшении Я.

Прибор, измеряющий амплитуду колебаний тока в колебательном контуре, обнаружит скачки - резкое жесткое изменение амплитуды для Я = Я1 при увеличении Я и для Я = Яо при э уменьшении Я. Явление протекает по-

См. [34-36].

") Равновесные реншмы, которым соответствуют состояния рав-повесия, естественно понимать в обобщенном смысле; например, режимы, связанные с наличием постоянной угловой скорости, постоянного тока и т. д., рассматриваются как равновесные режимы. При этом предполагается, что поведение рассматриваемой реальной задачи описывается после выбора надлежащей системы координат автономным дифференциальным уравнением, а равновесным режимам соответствуют состояния равновесия. Такие состояния равновесия, следуя Раусу и Ляпунову, называют также установившимися движениями.

") В характеристическое уравнение входят только коэффициенты линейных членов правых частей системы (А), поэтому такое исследование называется линеаризацией данной системы.

2) Условие отрицательности действительных частей характеристических корней в случае динамических систем любого числа измерений даны Раусом и Гурвицем в форме неравенств для ряда детерминантов. Для мно-

Однако эти понятия могут бьггь перенесены и на случай, когда фазовая плоскость дифференциального уравнения, описывающего тот или другой реальный объект, имеет более сложный вид, т. е. когда на фазовой плоскости существует не единственное состояние равновесия, а несколько и среди них есть седла, а значит, сепаратрисы. И в случае более сложной фазовой плоскости имеет смысл говорить о мягком и жестком возникновении колебаний, если описанная выше ситуация имеет место вокруг одного из существующих в системе фокусов.

Кроме того, очевидно, при большом числе предельных циклов у системы дифференциальных уравнений возможно резкое изменение амплитуды колебания, соответствующее тому, что изображающая точка при исчезновении одного цикла перескакивает на другой.

Рассмотренные случаи перескоков изображающей точки, вызванных бифуркациями, возникающими при изменении параметров, естественным образом привели к понятию «безопасных» и «опасных» границ области устойчивости.

§ 4. <<Безопасные» и «опасные» границы области устойчивости состояний равновесия"). Вопрос об устойчивости состояний равновесия (равновесных режимов)") возникает при решении многих прикладных задач (из области автоматического регулирования, гироскопической стабилизации, радиотехники, электротехники и т. д.).

Естественно предполагать (см. гл. 8, § 1), что в прикладных задачах соответствующая система дифференциальных уравнений (в частности ее состояния равновесия) грубая и что, следовательно, при анализе устойчивости можно ограничиться тем случаем, когда этот вопрос может быть решен путем отбрасывания всех нелинейных членов и исследования характеристического уравнения ") (состояние равновесия устойчиво, если действительные части характеристических корней отрицательны)2).