7) кривая проходит между точками Л(УЗ -1, Ул/2(1 - -УЗ/3)) и 5(1, Оу,

8) о =(4/13)У13 = 1,11...

Разбиения фазового пространства системы (9) с релейными характеристиками не будут для всех областей пространства па-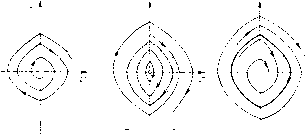

с<0

Рис. 247

раметров качественно эквивалентными соответствующим разбиениям для аналитических и полигональных характеристик, но будут в случаях различия сходными, допускающими отождествление в указанном выше смысле. Различие в бифуркациях будет на прямой 0 = 0 (рождение неустойчивого предельного цик-.ла при изменении знака о из границы некоторой области, содержащей внутри особую точку).

Разбиение пространства параметров о, V для системы с релейными характеристиками отличается от представленного на рис. 244 расположением кривой АВ. Точка А не лежит на оси о = 0. Кривая АВ касается в точке А границы области 2 при а = УЗ-1. На интервале 0< < о < УЗ - 1 возможен при возрастании V непосредственный переход, минуя область с двумя циклами от разбиения (см. рис. 245, а) к разбиению (см. рис. 245,д) через рождение неустойчивого предельного цикла от петли сепаратрисы, охватывающей цилиндр. Характер и взаиморасположение других бифуркационных кривых не изменяются при замене полигональных или аналитических характеристик релейными (рис. 248).

Рис. 248

§ 6, Динамическая система, описывающая симметричный полет самолета. Рассмотрим опять систему, изученную в гл. 16 § 4 и В § 1 настоящей главы:

d(pldt = у- cos (р, dy/dt = у{а - у - вшф), (15)

и введем малый параметр = р, а = k\i. Эта система (с малым р) рассматривалась в § 3 гл. 15. Напомним здесь некоторые факты. Нри р = О система имеет интеграл

Н{(р, y) = y/3 - ycos(p=-h. (16)

Замкнутые кривые семейства (16) прп -2/3</j<0 охватывают состояние равновесия, при О < ft < «> - фазовый цилиндр. Нри малом р система имеет три состояния равновесия: О,(-я/2,0) и С»2(я/2,0)-седла, С»з[(А:-1)р, 1 + (F- 1)р2/2] фокус (при р = о - центр). Фазовое пространство цилиндрическое. В соответствии с физическим смыслом переменных и параметров рассматриваем лихиь верхний полуцилиндр (у = 0 - интегральная кривая) и положительные значения параметров.

Особенность разбиения фазового пространства на траектории состоит в рассматриваемой задаче в том, что для значений параметров, при которых возникает сепаратриса, идущая пз седла в седло, образуются сразу два замкнутых контура, составленных из сепаратрис седла на цилиндре и отрезков оси ф: контур, охватывающий состояние равновесия, и контур, охватывающий фазовый цилиндр. От контуров, составленных из сепаратрис седла, при изменении параметра появляется либо предельный цикл, охватывающий состояние равновесия, либо предельный цикл, охватывающий фазовый цилиндр. Поэтому функция (ft), корни которой определяют структуру разбиения на траектории, может быть записана единообразно для циклов любой природы:

\p{h) = \ {k - 3y)dyd(p или (ft) = f y{k-y)d(f

соответственно для -2/3<ft<0 или 0<ft<oo, что можно для обоих случаев записывать в виде

(ft) = 2 (-yWl dy. (17)

Здесь ei и ег < ei - положительные корни уравнения у - - Зг/= 3ft, если -2/3<ft<0, или положительные корни соответственно уравнений у - Зг/ = 3ft и г/ + Зг/ = 3ft, если ft > 0. Функция ij3(ft) доопределяется для ft = -2/3 и ft = О ее предельными значениями.

Исследование обнаруживает, что ij3(ft) = 0 не может иметь более двух корней на интервале О < ft < «> и более одного корня для -2/3 <ft<0.

Все возможные бифуркации в системе (15) с малым параметром соответствуют следующему набору условий (каждому отвечает определенное значение к):

1. ф(-2/3) = 0, 1з(-2/3) = 0. При убывании к из состояния равновесия появляется неустойчивый предельный цикл.

2. ij3 (0) = 0. При убывании к из петли сепаратрисы появляется неустойчивый предельный цикл, охватывающий цилиндр, а ири возрастании к появляется неустойчивый предельный цикл, охватывающий состояние равновесия.

3. Tfi(ft*) = 0, 1з(й*) = 0 (ft*>0). При убывании к исчезает двойной предельный цикл. При возрастании к двойной предельный цикл разделяется на два (верхний - устойчивый, нижний - неустойчивый).

Перечисленному набору условий соответствуют следующие значения параметра к:

1) к = 3, 2) А; = Г4(1/4)/(8л2) = 2,188, 3) А; = 2,05.

Вид функций i)(ft) для различных к представлен на рис. 249. На рис. 250 в плоскости малых параметров а представлено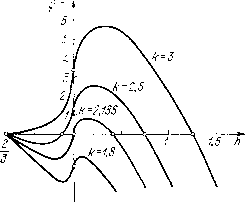

Рис. 249

Рис. 250

разбиение на области с различной качественной структурой разбиения фазового пространства на траектории. Заштрихована узкая полоса, для точек которой в фазовом пространстве есть два предельных цикла.

Рассмотрим систему (15) с малым параметром при аппроксимациях созф пилой, з1пф релейной функцией. 30*