Однако очевидно, что проведение всех указанных действии может быть осуществлено лишь в очень частных случаях. Иногда удается косвенными методами установить существование таких бифуркационных кривых и даже получить некоторые сведения об их расположении.

Укажем один из случаев, когда можно доказать существование в плоскости параметров бифуркационной кривой, соответствующей двукратному предельному циклу.

Предположим, что на некоторой части а кривой а* = О (кривая а* = О соответствует сложному фокусу) величина Li положительна, на части а" отрицательна и в точке М этой кривой, являющейся общим концом этих двух частей а и а", величина Li = 0. Если удается показать, что в точке М вторая ляпуновская величина L2 = as{X\)¥=0, то на основании общей теории (см. гл. 10) отсюда можно заключить, что при значениях параметров, соответствующих точке М плоскости параметров, динамическая система имеет сложный фокус второго порядка, из которого при изменении параметров могут появиться два (и не более) предельных цикла (см. гл. 10).

Принимая во внимание, что от сложного фокуса, в котором L\ < О, рождается устойчивый предельный цикл, а от сложного фокуса с Li> 0~ неустойчивый, и используя соображения непрерывного перехода от одних значений параметров к другим, в этом случае можно установить, что на плоскости парам1зтров существует бифуркационная кривая с концом в точке М, соответствующая двукратному предельному ци1шу (см. примеры гл. 16).

Если на плоскости параметров Ki, Я,2 точки бифуркационной кривой S соответствуют системам первой степени негрубости, имеющим один из указанных в гл. 9 негрубых элементов, то при изменении параметров вдоль какой-нибудь дуги, пересекающей кривую S, смена качественных структур будет одной из описанных в § 2 (при изменении Я, от Я, < Яо к Я. > Яо).

Особым точкам бифуркационных кривых или общим точкам различных бифуркационных кривых соответствуют динамические системы степени негрубости выше первой.

В то время как точки бифуркационных кривых, соответствующих системам первой степени негрубости, являются граничными для двух различных грубых областей пространства параметров, точки, соответствующие системам более высокой сте-

ствуюгцее периодическое решение), как функцию параметров, а также его период как функцию параметров и затем подставить это решение и период в выражение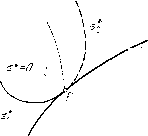

пени негрубости, могут быть граничными более чем для двух грубых областей. Поэтому нахождение точек пространства параметров, соответствующих системам степени негрубости выше цервой, и изучение поведения системы в окрестности таких значений параметра часто позволяют установить наличие целого ряда различных грубых областей с различными качественными структурами.

Остановимся на одном частном случае динамической системы второй степени негрубости, именно, динамической системы, имеющей двукратное состояние равновесия, для которого а = 0 (см. гл. 10, § 4). Можно показать, что все бифуркации этого состояния равновесия могут быть получены при изменении

двух независимых параметров. В пространстве этих параметров - мы их будем обозначать через ki и Яг - такому со- Aff стоянию равновесия соответствует общая точка кривых

А*(Я1, Я2)=0 и а*(Я1, Я2) = 0.

Можно показать, что при значениях параметров, соответствующих этой точке (рис. 108), кривые А* = О и а* = О касаются в точке Р. При этом всем отличным от Р точкам А* соответствуют седло-узлы, но точ-Рис. 108 кам кривой А*, лежащим по

одну сторону точки Р,- седло-узлы с устойчивой или соответственно неустойчивой узлово!! областью, а по другую сторону Р - с неустойчивой (устойчивой) узловой областью. Кривая а* = О точкой Р делится на две части: а* и а*. Одной (а)соответствует сложный фокус (сплошная линия на рис. 108), другой - седло, для которого Ос = 0. Между двумя ветвями кривой а* = О лежит кривая I (упирающаяся в точку Р), соответствующая петле сепаратрисы.

§ 4. Бифуркации «от бесконечности». В § 2 рассматривалась смена качественных структур, которая происходила вблизи негрубого особого элемента (сложной особой точки, сложного фокуса и т. д.), лежащего внутри области определения динамической системы. Очевидно, можно также рассмотреть и возможные смены качественных структур в том случае, когда негрубый особый элемент лежит на границе области определения динамической системы. Не останавливаясь на случае, когда система (А) определена в ограниченной части плоскости, укажем некоторые возможности бифуркаций «от бесконечности» в случае, когда

система

dx/dt = P{x, уЛи -Лп), dy/dt = Qix, у, Ки

определена на всей плоскости. В этом случае при изменении параметров от некоторых фиксированных значений Я" возможно, например:

1. Появление состояния равновесия из бесконечности. Пример 1.

х = у-{1 + е)х, у х-у - \.

При е = О у системы нет состояний равновесия, при г ФО (но сколь угодно малом) появляется состояние равновесия с координатами х = -1/е, у = -1/е - 1.

2. Рождение предельного цикла из бесконечности).

Пусть в системе (А) при значении параметра бесконечность устойчива. Это означает, что все траектории, проходягцие вне окружности достаточно большого радиуса, уходят в бесконечность.

Пусть далее при значениях Я, > Яо (или Я < Яо) бесконечность делается неустойчивой, т. е. все траектории, проходягцие вне окружности достаточно большого радиуса, входят внутрь этой окружности. Нетрудно видеть, что тогда при Я > Яо (Я < Яо) суш;ествует устойчивый предельный цикл и этот цикл при Я Яо уходит в бесконечность.

Естественно считать, что этот цикл «рождается» из бесконечности. Очевидно, из бесконечности может также родиться неустойчивый предельный цикл.

Пример 2.

Л = -1/-Ьж-Я(х2-Ь1/2)х,

у = Ж-Ь1/-Я(х2-Ь1/2)1/.

При я = о мы получаем линейную систему х = -у-х, у = х + у

с единственным неустойчивым фокусом в начале. Если составить выражение

d(x + y)/dt = 2хх + 2уу = 2(х + у),

то нетрудно видеть, что бесконечность устойчива, так как все окружности являются циклами без контакта и траектории при возрастании t выходят из этих окружностей.

) В случае, когда правые части динамической системы (А) - многочлены, так что систему можно рассматривать па сфере Пуанкаре (см. гл. 6), бифуркациям от бесконечности соответствуют бифуркации от экватора сферы Пуанкаре. При этом, очевидно, необходимо ввести понятие грубости системы па сфере Пуанкаре и условия грубости и пегрубости экватора. Однако в настоящей книге эти вопросы не рассматриваются.

13»