
 |
|
Главная страница Приемы качественного исследования [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [ 108 ] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] / 1 <р(ж)) = 0. (2) Решить это трансцендентное уравнение относительно х сложно. Мы поступим иначе: именно, рассмотрим вспомогательную плоскость (х, уо)). На этой плоскости соотношение (2) определяет семейство кривых, зависяш;их от параметра Xq, y,= F {x, x,) = - 0 (1 - ))- (3) Кривые (3), соответствуюш;ие различным xq, как нетрудно видеть, не имеют обш;их точек. При каждом фиксированном xq абсциссы точек пересечения соответствуюш;ей кривой (3) с некоторой данной прямой уо = С являются абсциссами состояний равновесия системы (1). В рассматриваемой задаче имеет смысл лишь значение х, a<x<i, где а - корень уравнения 1х + х~ 1 = 0. (4) Это вытекает из того, что при у +°о Р{х,у)== -Ххе-" +1-х = 0 обращается в (4). Значения х> 1 также не имеют смысла, так как из Р{х, у) = 0 при значениях х> 1 мы получаем что, очевидно, невозможно (е"-> О всегда). (Отсюда следует, что изоклина Р{х, у) = 0 целиком лежит в полосе axl.) Из выражения для F(x, xq) следует, что для каждой из кривых (3) г/о(а)=+«>, г/о(1)=0. Далее, можно показать, проводя элементарные вычисления, что вторая производная от функции F{x, xq) обращается в нуль 5) Использование такой вспомогательной плоскости (один параметр и одна координата) не является частным приемом, и, как правило, естественным образом используется в разных задачах. му решение вопроса о возможном числе состояний равновесия требует специального рассмотрения. Найдя из соотношения Р{х, г/) = - Яа;"е~+ (1 - а;) = О величину = 1 1 1 - ж и подставляя это выражение в Q{x, i/) = 0, находим, что абсциссы состояний равновесия удовлетворяют соотношению только один раз при значении аг, являющемся корнем уравнения 1 - ?г 4-2гаж - (ге - 1) 2[n{i~x)+xf Отсюда следует, что каждая из кривых (3) имеет не более двух экстремумов и пересекается с любой из прямых уо = С не более чем в трех точках. Система имеет, следовательно, не более трех состояний равновесия. Рассмотрим, какие из состояний равновесия - узлы и фокусы и какие - седла. Дифференцируя по X выражение (2), где г/ = 1/ф(а;) есть решение уравнения d 1 Р{х, г/) = 0, п принимая во внимание, что -- = """р" лучаем - liFx = Qx <f{x) (p{x) j dx ф(г) (f(x) ф(ж) - A f, V ф(ж) / ф(ж) где Ру [х, j < О и А (а;, г/) = PQy - QxPy Таким образом, знак Д(аг, у) при заданных и г/о в состоянии равновесия, имеющем абсциссу х, иротивоноложен знаку производной В точке кривой (3) с тем же а; и у о. Рассмотрим на плоскости {х, г/о) кривую, являющуюся геометрическим местом экстремумов кривых (3). Эта кривая очевидно получается, если мы исключим аго из уравнений Уо = Р{х,Хо) ш Рх{х,хо) = 0. (6) Уравнение этой кривой будет 0 - ф(ж) п{1-х) Н- X(f (х) = lfix). Ее ВИД установлен в приложении I. Она пересекает ось х при некотором значении Xi> а>0. Будем обозначать через А* часть кривой (7), лежащую над осью х (только эта часть рассматривается при сделанных предположениях относительно возможных значений переменных и параметров). На рис. 170 изображено семейство кривых (3) (тонкими линиями) и кривая А* (сплошной ТОЛСТОЙ линией). Из выражения для F{x,xo) следует, что большему значению хо соответствует ниже находяш;аяся кривая (3). Если Хо мало, то кривая (3) расположена высоко, не пересекает кривую Д* и не имеет экстремумов. При больших Хо кривая (3) пересекает линию Д* и имеет в точках пересечения максимум и минимум. Нетрудно видеть, что для точек иод 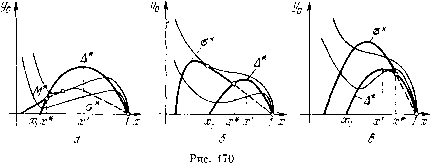 линией А* знак Fx{x, х) положителен (см. формулу (5)), состояния равновесия - седла, а для точек над линией А* знак fx {х, Хд) отрицателен, состояния равновесия - узлы или фокусы. В точках линии А*, в которых Fx{x, Хд)= О, соответствующие состояния равновесия кратные, причем в точках линии А*, не являющихся максимумом этой линии,- двукратные, а в точке, являющейся максимумом,- трехкратное. Перейдем к выяснению устойчивости узлов и фокусов и установлению знака седловой величины в седле. Для этого выразим для каждого состояния равновесия а=-Р;-(?; (8) через координаты этого состояния равновесия. Для этого из выражений Р{х, у) = 0, Q{x, j/) = 0 выразим у ш Хо через х и остальные параметры. Мы получим о =. Р1/оФ(х) - РФ(.) + "(1-- + (1 + И Рассмотрим на плоскости (х, г/о) кривую о = О, т. е. кривую цх<р2 {x) fix). Нетрудно установить, что эта кривая на плоскости (х, уо) имеет вид, представленный на рис. 170 (см. приложение П). Часть кривой, лежащей над осью х, будем обозначать через о*. [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [ 108 ] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] [130] [131] [132] [133] [134] [135] [136] [137] [138] [139] [140] [141] [142] [143] [144] [145] [146] [147] [148] [149] [150] [151] [152] [153] [154] [155] [156] [157] [158] [159] [160] [161] [162] [163] 0.0098 |