Ниже перечислены все возможные типы состояний равновесия с не равными нулю действительными частями характеристических корней и приведены схематические рисунки расположения траекторий в их окрестности.

При этом для недикритического узла и для седла рисунки приводятся как в случае, когда рассматриваемая система имеет канонический вид (когда направления, по которым к состоянию равновесия стремятся траектории, совпадают с направлением осей координат), так и в общем случае (т. е. в случае, когда система не имеет канонического вида, так что направления ki и /с2 могут быть любыми).

I. Узел (характеристические корни Xi и Х2 действительны и одинаковых знаков, т. е. > 0; А > О, - 4А > 0).

А. Невырожденный узел (Xi ¥= Х2):

а) устойчивый: Xi < О, Хг < О, т. е. о<0 (рис. 41, 44);

б) неустойчивый: Xi > О, Хг > О, т. е. о > 0.

(Рисунки даются только для устойчивого узла, в случае неустойчивого узла надо переменить направление стрелок. При этом

рис. 41 соответствует случаю, когда система имеет канонический вид, а рис. 44 соответствует общему виду.)

Б. Вырожденный узел (Xi = Хг = X, но в канонической форме р, =5 О, А > о,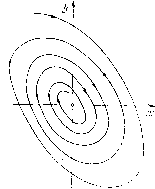

о2-4А = 0):

(рис. 43,

Рис. 50

а) устойчивый: X < О 45);

б) неустойчивый: X > 0. (Рис. 43 соответствует случаю, когда система имеет канонический вид, а рис. 45 соответствует общему виду.)

В. Дикритический узел (Xi = Хг =Х и IX = 0):

а) устойчивый: Х<0 (рис. 42);

б) неустойчивый: Х>0.

П. Седло (характеристические корни Xi и Хг действительны и разных знаков, т. е. XiX2 < О, либо Xi > О, Хг < О, либо Xi < О, Хг > О, А < 0) изображено на рис. 46 и 47 (рис. 46 соответствует случаю системы в каноническом виде при Xi > О, Хг<0, рис. 47 - общему случаю).

111. Фокус (характеристические корни комплексные сопряженные, т. е. А > О, 0 - 4А < 0):

а) устойчивый: а < О (о < 0) (см. рис. 48 и 49 для устойчивого фокуса в случае канонического вида системы: рис. 48 соответствует случаю Р > О, рис. 49 - случаю р < 0; рис. 50 соответствует случаю, когда система имеет общий вид);

б) неустойчивый: а > О (о > 0).

Пример 1.

х = У, у = х{а - х)+ by.

Состояние равновесия 0(0, 0)-седло. Определим направления сепаратрис в седле. Уравнение для нахождения углового коэффициента сепаратрис в седле имеет вид - Ък - а? = О, откуда А;, 2 - 6/2 ± ГЬ2/4 + а?. Пример 2.

х==-х{2 + у), г/ = а;+рг/.

Состояние равновесия 0(0, 0)- седло. Уравнение для определения направлений сепаратрис в седле: ( + 2)/с-Ь 1 = О, откуда к = -1/(2+ Нетрудно видеть, что второе значение к есть о, а сепаратриса с наклоном к = оо есть прямая х = 0.

ГЛАВА 4

КАЧЕСТВЕННАЯ СТРУКТУРА ОКРЕСТНОСТЕЙ НЕКОТОРЫХ СЛОЖНЫХ СОСТОЯНИЙ РАВНОВЕСИЯ

§ 1. Направления, в которых траектории стремятся к сложному состоянию равновесия. При исследовании сложных состояний равновесия иногда бывает весьма существенно знание направлений, в которых траектории могут стремиться к этому состоянию равновесия ).

Рассмотрим динамическую систему

dxldt = Р {х, у), dyldt = Q {х, у),

для которой начало координат является сложным состоянием равновесия, так что

(0,0)= О, (3(0, 0)= О,

р;(о,о) р;(о,о)

;(0,0) Qy (0,0)

Предположим, что разложения правых частей в ряд по степеням X, у в окрестности точки 0(0, 0) имеют вид

Р(х, у) = Рт(х, !/) + <p(x, у),

Q{x, y)Qrn(x, у) + (х, у),

где т> i, Рт(х, у) и Qm(x, у)- однородные многочлены, состоящие из всех членов т-го порядка соответствующих разложений, а функции (р(х, у) и \j)(a;, у) - ряды, состоящие из членов более высоких порядков. При этом мы считаем, что многочлены Рт(х, у) и Qm(x, у) одновременно не равны тождественно нулю (в противном случае мы бы взяли т > т). Рассмотрим выражение

xQm(x, у)-уРгп(х, у), (2)

а также выражение

Qr.(i, k)-kP(i, к),

= 0. (1)

) Методы исследования сложных особых точек (метод Бендиксона [143] и метод Фроммера [132]) опираются на рассмотрение траекторий, стремящихся в определенном направлении.