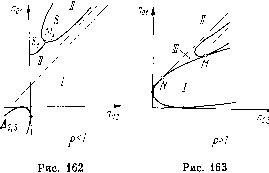
р>1

Рис. 164

Для того чтобы получить на плоскости (reoi, геог) кривую, соответствующую 0 = 0 (смене устойчивости), нужно исключить /га и ге из уравнений

а(/га, ге)=0, Р{т, ге)=0, Q{m, п)=0.

Однако такое исключение весьма сложно, и проще получить параметрические уравнения этой кривой. Исключая п из

получаем

Р{т, п)=0, Q{m, п)=0, noi{pm + 1)-По2{т + 1) -(р/га + 1) (т + 1)= О

(12)

и, полагая в (10) n = noi/{m+ 1), с помощью (10) и (12) выражаем по1 и по2 через /га (/га - параметр):

(m + l)(pm+l) , , 1

«03= "v;: (13)

Кривую на плоскости (reoi, /гог), определенную равенствами (13), или, что то же, уравнениями (11), будем обозначать через S. Исследование характера этой кртой при разлЕЕчных р и G даны в приложении I. Некоторые основные случаи ее характера и расположения относительно кривой Дгз даны на рис. 162-164. Из исследования в приложении I следует, что: 1) кривая S имеет ветви, уходящие в бесконечность при /га-0 и 7?г->оо, и при имеет асимптоту (штриховая прямая на рис. 164); 2) при р> 1 кривая S имеет одну общую точку М с кривой Агз, соответ-20*

где вместо /га и ге подставляются координаты соответствующих состояний равновесия. Из (9) мы, очевидно, получим (после некоторых преобразований) те же условия (7) и (8), соответствующие наличию у системы кратного состояния равновесия.

ствующую значению т = т. Нетрудно убедиться на основании выражений (9) и (10), что:

A) Состояние равновесия Oi - седло, когда uqi - щч, - 1 > О, и устойчивый узел, когда по\ - иог - 1 < 0.

Б) В случае р < 1 состояние равновесия Ог, для которого 0 = 0, всегда сложный фокус. В случае р > 1 состояние равновесия, в котором а = О, есть сложный фокус Ог для т<т (т. е. для ветви AM кривой S) и седло Оз для т> т (т. е. для ветви MB кривой S).

B) Нри р > 1 для значений параметров, соответствующих точке М, система имеет двукратное состояние равновесия, для которого а = 0. Это состояние равновесия рассмотрено в § 4 гл. 10. В точке М кривая S касается кривой Аг» (это вытекает из сказанного в § 3 гл. 11 и может быть также получено непосредственно, если для параболы, как и для кривой S, найти параметрические уравнения). Точкой М кривая (Агз) разделяется на две части. Точки одной соответствуют системе (1), имеющей седло-узел с устойчивой узловой областью, а точки другой части - с неустойчивой узловой областью. На рпс. 162-164 штрихами указаны области, где состояние равновесия Ог соответственно устойчиво (о < 0) и неустойчиво (а>0). Очевидно, ири переходе в плоскости (иоь Йог) через кривую S у системы (1) возможно рождение предельных циклов, на котором мы остановимся ниже.

Предельные циклы. Покажем сначала, что существует замкнутая область в фазовом пространстве, содержащая все состояния равновесия, внутрь которой входят траектории системы. Действительно, рассматривая прямые Ti: и = О, Гг:?г = ?го1, можно показать, что все траектории входят внутрь полосы, ограниченной этими прямыми.

Рассматривая поле направлений на прямой Гз: т = Ci, где Ci - некоторая положительная постоянная, для raoi 1 получаем, что траектории пересекают эту прямую сверху вниз. Таким образом, для по1 < 1 существование замкнутой области показано, а для по1 < 1 необходимо еще рассмотреть иоле направлений на прямой Г4: т = - G{noi - 1)п +С2. Выбирая Сг достаточно большим, можно убедиться, что на интервале i < щ noi траектории пересекают эту прямую справа налево, т. е. по-прежнему существует область, внутрь которой входят все траектории системы (1).

Принимая во внимание тот факт, что существуют значения параметров, при которых система имеет одно состояние равновесия, лежащее на интегральной прямой пг = О, а также принимая во внимание, что состояние равновесия О3 - седло, можно утверждать:

а) если предельные циклы существуют, то они обязательно ох ватывают состояние равновесия Ог;

б) предельных циклов в области значений параметров /, включая границы - прямую (7) и кривую (8), быть не может;

в) так как существует область фазового пространства, внутрь которой входят все траектории системы и, кроме того, при переходе из области значений параметров в область состояние равновесия о2 (лежащее выше интегральной прямой /га = 0) меняет устойчивость, то должен существовать по крайней мере один устойчивый предельный цикл.

Мы покажем, что в некоторых случаях у системы может существовать два предельных цикла. Рассмотрим выражение для первой ляпуновской величины (полученное в приложении II)

я (т -f-1) /(m)

L (т) =

4Д Уд т (рт + 1)

где /(/ra) = p(p+Gp - 1)/п2 + 2(р - l-Gp)7ra + p+l.

1) р < 1. В этом случае, очевидно, существует не более двух состояний равновесия, седло лежит на прямой т = О, и, очевидно, его сепаратрисы не могут образовать петлю (рис. 165).

Возможны два случая:

а) р - 1 + Gp < 0. Уравнение /(/га)= О не имеет положительных корней, L{m)< О при всех /га.

б) р - 1 + Gp > 0. Граница области устойчивости S состоит из двух участков, на одном пз которых L < О, на другом L > 0;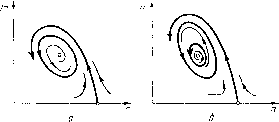

Рис. 165

в точке Мз, граничной для этих участков, L = 0. В точках, где L<0, при переходе из области, где о < О, в область, где о > О, у системы из фокуса рождается устойчивый предельный цикл, а в точках, где L > О, при обратном переходе из области, где о > О, в области, где о < О, рождается неустойчивый предельный цикл.

Особенности в поведении системы в окрестности тех значений, при которых L = О, можно выяснить, устанавливая знак второй ляпуновской величины L2. Однако мы можем рассмотреть возможности, которые здесь могут иметь место и без вычисления втой величины.