рассуждения, проведенные в гл. 16, § 4, так как при изменении р, осуществляется монотонный поворот поля направлений, а принятая аппроксимация (4) не изменяет существенно поведения величин Оз, аз и 04, определяющих характер возможных бифуркаций в окрестности фокуса н петли сепаратрисы. Для аппроксимирующей системы, как н для исходной системы (2), При (X+i)/yi<l предельных циклов нет и все бифуркации осуществляются па отрезке Л = = const между граничной кривой и прямой р = Л -Ь 1. Характер разбиений пространства параметров и фазового пространства при аппроксимациях (4) остается таким же, как и для исходной системы (2) (рис. 233). (Ср. рис. 233 и 167.)

§ 3. Рассмотрение системы (2) при аппроксимациях кусочно-постоянной для sin<p, и пилообразной для cos<p функциями. Полагаем

Рис. 233

Sin ф ~ S4 =

-1, (-п,0), 1, (О, л).

cos ф

с. =

2п~\ + 1, 1-2л~Ф+ 1,

[-л,0], [О, л]

(см. рис. 234 и рис. 229 нижний).

Заметим, что это - интегрируемая аппроксимация. Правая часть системы (2) при аппроксимациях (5) терпит разрыв на линиях сп1ивапия. Кроме прямой р = О, роль изоклины горизонтальных наклонов вьшолняет ломаная, состоящая из кусков интегральных прямых р = (Л-Ь1)/р, = рз, (-Л, 0), р=(Л-1)/р = р4, (О, л) и отрезков между ними ф = О, ±л, (Я - 1)/р, < р <(Л-Ь 1)/р,, па которых производная меняет знак. При (Я - 1)/р, > 1 иа полосе -л < ф < л будет только два состояния равновесия: Oi[(-л/2, 0)-седло и 02(л/2, О)-неустойчивый узел. При (Л-1)/р = 1 изоклины смыкаются и возникает сшитая сложная особая точка (О, 1), качественно эквивалентная вырожденному седло-узлу без узловой области (гл. 4) (рис. 235). При (Л-1)/р,<1 сложная особая точка распадается на две: Оз(0, 1)- сшитый фокус и 04(ф4, Р4)- седло. При (ЯЧ!)/!! 1

Рис. 234

фокус Оз превращается в устойчивый узел Оз(фз, рз). Границей области существования двух и четырех точек будет прямая к - - ц, - 1 = 0. На прямой А = 1 сливаются точки О4 и О2.

1. Рождение предельного цикла из сшитого фокуса. Сшитый фокус будет устойчив, если будут иметь разные знаки величины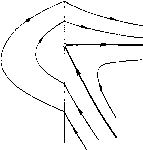

/20 (0,1) /ip(0,l)\

2d(0,1) Ло(0,1)

<?1(0,1) = 2(А-ц+1).

Здесь 71(ф,р) = С1 (ф«гО)и 72(Ф,Р) = = Сг (ф 0)- общие интегралы системы (см. гл. 17, § 4, п. 2).

Сшитый фокус меняет устойчивость на кривой

Рис. 235

«2=1"

(1 + Я) Ц - Я

= О,

(А, - ц + 1) (Я - ft - 1) начинающейся в точке (ц, = (1 + л)~, % = = 1) и заканчивающейся на граничной прямой в точке (ц = л~, А = (1 + л)л-).

При переходе через кривую аг = О в направлении возрастающих \1 сшитый фокус из неустойчивого становится устойчивым, и из него появляется неустойчивый предельный цикл (величина а4 - аналог первой ляпуновской величины L\ - для точек бифуркационной прямой (14-л)ц, - А = 0 положительна).

2. Раз!биение пространства параметров на области с различной качественной структурой фазового пространства. Вдоль всей граничной кривой характер сложной особой точки и структура разбиения фазового пространства на траектории сохраняются. Бесконечность неустойчива; а-сепаратриса седла 0\ не может идти в особую точку и накручивается на устойчивый предельный цикл, охватывающий цилиндр. Качественная картина разбиения на траектории на всей граничной кривой эквива.лентна изображенной на рис. 168, - /.

При (А4-1)/ц,<1 со-сепаратриса седла О4, входящая в особую точку по направлению к = -2л- - 2р., попадает при ф = О в область отрицательных наклонов и идет в бесконечность. Предельных циклов нет. Качественная картина эквивалентна изображенной на рис. 169, 8. Обращение в нуль седловой величины

= + <?р)4 = 2Л-Ч1 + л - Хл)

происходит на прямой Я.=(1 4-л)/л, смыкающейся с линией, на которой фокус Оз меняет устойчивость, в точке пересечения с граничной прямой А - ц. - 1 = 0. Седловая величина отрицательна выше прямой 04 = 0.

Отправляясь от известных структур разбиения фазового пространства на граничной прямой и в области Я. - р + 1 < О, опять легко проследить все бифуркации и смену качественных структур при монотонном повороте векторного поля с возрастанием параметра р.

Последовательность качественных структур, переходящих одна в другую при возрастании р, эквивалентна представленным на рпс. 169 последовательностям грубых структур 2-8 (если 1 < Я. < < 1 -Ь л~) или структур 2, 5, 6,8 (если 1 + л~ < Я). Негрубые структуры, разделяющие перечисленные грубые, также качественно эквивалентны негрубым, представленным на рис. 169, за исключением структур 2-3 и 2-5 (последней нет на рис. 169), которые должны быть заменены структурой - / рис. 168 (вместо седло-узла с неустойчивой или устойчивой узловой областью будет вырожденный седло-узел).

Качественная структура разбиения пространства параметррв отличается от структуры разбиения для исходной системы (2) лишь тем, что бифуркационные кривые 5-6 и 6-8 не пересекаются с граничной кривой 2-5 и уходят в бесконечность (рис.236).

Малым изменением аппроксимации (5) можно получить картину разбиения пространства параметров, качественно совпадающую с разбиением для исходной системы (2). Рассмотрим систему (2) при аппроксимациях

(-1,

sin ф

COS ф ~ Cj =

1+1,

(-л, - Фо), [-Фо. Фо].

[фо.л];

[-Л, 0], [О, л]

(см. рис. 237 и 229 нижний), отличающихся от (5) аппроксимацией з1пф на интервале (-Фо, фо). При малом фо аппроксимация (6) близка к (5). Точки Oi(-л/2, 0) и 02(я/2, 0) будут иметь такой же характер, как и при аппроксимации (5). На прямой Я = 1 сливаются точки 0 и 0. Граничной кривой, на которой сливаются точки Оз и О4, будет ломаная, составленная из двух звеньев: отрезка прямой Я = (1 - 2я~фо) р + 1 для 0<:р<(л/2)ф7 29 н. н. Баутин. Е. А. Леонтович