Если, выйдя из достаточно близкой к прямой (7) точки, в которой, как мы уже говорили вытне (см. н. б)), нет предельных циклов, мы перейдем из области а < О в область а > О через участок кривой S, где L<0, то при этом у системы рождается устойчивый предельный цикл. Пока мы не пересечем вновь кривую S, этот устойчивый предельный цикл сохранится - ему некуда деться (если в области а > О есть точки, соответствующие двукратным циклам, то тогда во всяком случае число устойчивых циклов все время будет на единицу болыне, чем неустойчивых). Если затем мы пересечем границу S на части ее, где L > О, переходя из области а > О в область а < О, то при этом у системы из фокуса рождается неустойчивый предельный цикл, устойчивый же сохраняется, и таким образом теперь у системы есть устойчивый и неустойчивый предельные циклы (или одинаковое число и тех и других).

Если, не пересекая кривую S, мы вернемся в область вблизи прямой (7), где нет предельных циклов, то мы непременно должны пройти через значения параметров, при которых эти предельные циклы исчезают. Следовательно, должна бьггь бифуркация, при которой устойчивый и неустойчивый циклы сливаются, образуя четнократпый цикл, который затем исчезает. Пепременпо существует, следовательно, в области параметров, где а > О, бифуркационная кривая Sl, упирающаяся в точку Mz, соответствующая четнократному циклу (см. рис. 162).

Возможные качественные структуры на фазовой плоскости представлены на рис. 165.

2) р > 1. В этом случае у кривых Агз и S есть общая точка М (предположим, что она лежит на части S, где L<0). При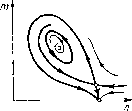

Рис. 166

значениях noi и пог, соответствующих этой точке, у системы есть двукратное состояние равновесия, для которого о == 0.

Бифуркации такой точки описаны в гл. 10. В частности, при бифуркациях такой точки (при наличии двух независимых параметров) всегда появляется петля сепаратрисы, а также предельный цикл (см. рис. 105 гл. 10).

) Нри то оо у кривой S асимптота не существует.

На плоскости (fZoi, 02) существует упирающаяся в точку М бифуркационная кривая Si, соответствующая петле сепаратрисы (см. рис. 108 гл. 11).

Существование такой кривой, т. е. существование петли сепаратрисы у системы (1) при некоторых значениях reoi и геог можно также установить, не опираясь на рассмотрение § 4 гл. 10, рассматривая возможное поведение двух сепаратрис седла О3 (по расположению изоклин, а также по характеру состояний равновесия вблизи участка кривой Агз) и переходя при непрерывном изменении параметров от расположения, представленного па рис. 166, а, к расположению, представленному па рис. 166, б. Здесь также можно установить существование двух предельных циклов, однако соответствующее рассмотрение (более сложное, чем в случае р< 1) мы здесь пе приводим. На рис. 166 представлены некоторые разбиения фазовой плоскости.

Приложение I. Установим возможный характер кривой S, пользуясь ее параметрическими уравнениями (13): reoi = Ф(та), пог = ф(та).

1. При и т--\-оо обе функции ф(та) и i)(to) стремятся к бесконечности. Нетрудно видеть, что производные

, 1 2рт -К2р + 1 + Gp) - 1 , 1 (рт + i) (2рт+рт ~ i)

обращаются в нуль не более чем при одном значении т, О < то < -- оо. (Среди коэффициентов полиномов, стоящих в числителе, только одна перемена знака, а при то = О и то = оо эти полиномы имеют разные знаки. Следовательно, у кривой S только по одной точке, в которых касательная к S соответственно горизонтальна и вертикальна. Соответствующие значения т

мы будем обозначать mmln ф и тотш

Вид кривой зависит от соотношения между тот1п ф и тот1п Вычисляя производную (f(m) в точке S, получим (используя условие

, 1-P + (1-P + Gp) то,„

ч™(-тшф) =-щ;;;-. (14)

Знак этого выражения позволяет судить о соотношении меяаду тот1п * и

тот1пф. Если ф(тт1п ,) < о, ТО TOmin if < TOmin ф И НаобороТ, еСЛИ

<P(TOmin<!i) > 0. Знак выражения (14) в свою очередь определяется соотноше-нием между TOmin ,1 и значением то = q, при котором числитель

выражения обращается в нуль, а соотношение между тотш * и то определяется знаком i)(m). (Отметим, что в случае m > О то-это значение, при котором кривые S и д23 имеют общзгю точку.)

2. Ветвь кривой S, уходящая в бесконечность при то О, имеет асимптоту (которую просто найти обычным образо.м) )

п -п (1-P + Gp) . ,,,,

"01 "ог -Щ-= 0. (15)

Значение то, соответствующее точке пересечения кривой S с асимптотой

(оно находится из (9) и (15)), есть

1 - р + G

" = -Т(Г-

На основании изложенного можно установить характер кривой 5 и ее расположение относительно кривой Дгз. Рассмотрим некоторые основные случаи.

1) р < 1. В этом случае асимптота кривой S лежит вьппе прямой Ио! -

п / 1 - р + Gp \ пог - 1 = О / так как--> 11, а кривая S целиком расположена

выше асимптоты (так как выра.кепие (16) для т отрицательно). Кроме того, mmin ч, > m (m < 0), откуда ф(тт1п г),)=1 - р-1-(1 - р + Gp)mmin * >

> О, и, следовательно,

Мы имеем случай, представленный на рис. 162.

2) р > 1. В этом случае кривые Дгз и S всегда имеют общую точку М, а асимптота кривой S лежит ниже прямой tioi - «02 - 1 = 0.

А) Пусть 1 - р2 + Gp > О, т. е. кривая S имеет общую точку с асимптотой:

а) ф (т) > О, т > 0. Отсюда Ш > min ф и

4>(mmin,t) = 1 - р + (1- р + Gp)mn,in « < 0.

Следовательно, Шш-щ ф < mmin а также т > mmin ф. Мы получаем расположение, представленное на рис. 163.

б) (т) < 0. Тогда гашш >гпш

ф("т1п ф) = 1 - р + (1 - р + Gp) mmin ф > О,

т. е.

TOmln ф > TOmin ф > ТО. (17)

В силу (16) у кривой S существует единственная общая точка с асимптотой, и при точки кривой 5 лежат выше асимптоты, а при т-*--оо - ниже. Но тогда, принимая во внимание (17), нетрудно видеть, что кривая S непременно должна иметь не менее одной точки самопересечения. Можно показать, что эта точка единственная. Действительно, для значений т и та", соответствующих точке самопересечения {т ф т"),

ф(т) =ф(т"), Щт)=р{т").

Подставляя сюда выражения для ф(т) и (т), после элементарных преобразований и сокращения на т - т" (т Ф т") получаем

Qmm"(m + т") + (2р + 1 + Gp) тт" + 1=0, (18)

ртт"{т + т") + (2р + р") тт" +1=0. (19)

Вычитая из (19) домноженное на р (18) и находя из получившегося выражения и из (18) тт" и т + т", получаем

1 - р - gp - 1

=-p(l-p-Gp)- "» + ""= p(l-p) •

Отсюда следует, что для существования точки самопересечения необходимо, чтобы т и т" были положительными корнями квадратного уравнения

2 , (1 -p + Gp) 1-Р „

р(1 р) -p(i p + Gp) = 0. (20)

Очевидно, не может существовать более двух значений, удовлетворяющих (20), и следовательно, более одной точки самопересечения (см. рис, 164),