топологическую структуру), если существует такая окрестность и ТОЧКИ О, не содержащая других состояний равновесия системы (А), что, сколь малое е > О мы бы ни взяли, можно указать такую область и , целиком лежащую в е-окрестности О, и такое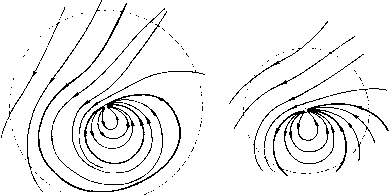

Рис. 30

топологическое отображение и на и, при котором траектории отображаются в траектории ).

Всякая область и, обладающая указанными в приведенном выще определения свойствами, называется собственной окрестностью состояния равновесия.

Как и всюду выще, предположим, что число особых траекторий рассматриваемой системы (А) в случае, когда система определена в ограниченной области, конечно в этой области, а в случае, когда эга система определена на всей плоскости, конечно во всякой ограниченной области плоскости.

Установим при этом предположении возможный характер собственной окрестности состояния равновесия.

Из теоремы 7 ири сделанном предположении следует:

Если в любой сколь угодно малой окрестности состояния равновесия О лежит замкнутая траектория, то все траектории, про-

Нетрудно привести пример состояния равновесия, не имеющего определенной топологической структуры в указанном выше смысле. Пусть, например, вокруг данного состояния равновесия существует бесчисленное множество вложенных друг в круга колец, заполненных замкнутыми траекториями. Пусть эти кольца перенумерованы в порядке их вложения друг в друга. Предположим, что между ге-м и ге -f- 1-м кольцом лежит п предельных циклов. Нетрудно убедиться, что у такого состояния равновесия нет определенной топологической структуры в смысле данного в тексте определения. Такой пример возможен в динамической системе класса С", но невозможен в аналитической системе.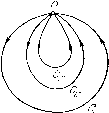

ходящие через точки некоторой достаточно малой окрестности О, замкнуты.

Состояние равновесия в этом случае называется центром.

Рассмотрим случай, когда в любой сколь угодно малой окрестности состояния равновесия О нет замкнутых траекторий. Пусть Zo - окружность с центром в точке О столь малого радиуса го, что внутри Zo, кроме О, не лежит целиком ни одна особая траектория.

Можно показать, что всякая положительная или отрицательная полутраектория, целиком лежащая внутри такой окружности, стремится к состоянию равновесия О.

Если существует окружность Со радиуса го такая, что все траектории, проходящие через точки внутри некоторой окружности С радиуса г го при t-* +0° -00), не выходя из Со, стремятся к состоянию равновесия О, а при убывании (возрастании) t выходят из Со, то состояние равновесия О называется топологическим узлом.

Узел в примере 3 и фокус в примере 4 являются топологическими узлами.

Теорема 17. Если состояние равновесия О есть топологический узел, то в любой сколь угодно малой его окрестности можно указать цикл без контакта, содержащий это рд,, 3

состояние равновесия внутри.

Рассмотрим состояние равновесия, не являющееся топологиче-ческим узлом.

Предположим, что существует траектория L, которая, не выходя из окружности С, стремится к состоянию равновесия прн

f -> + оо и при t - °о.

Пусть Сь - замкнутая кривая, состоящая из траектории L ж точки О (рис. 31). Нетрудно показать, что всякая траектория L, проходящая через точку внутри Сь, стремится при t + °о ж f - оо к состоянию равновесия О и вместе с точкой О образует простую замкнутую кривую Cl- При этом каждая из двух областей, ограниченных двумя различными такими кривыми Сь п Ci", лежит одна внутри другой.

Область, ограниченная кривой Сь, называется эллиптической или замкнутой узловой областью и обозначается через N,. Две эллиптические области считаются различными, если они лежат одна вне другой.

Рассмотрим теперь две стремящиеся к состоянию равновесия полутраектории L\ и L2, имеющие точки вне окружности С (каждая из этих полутраекторий может быть как положительной, так и отрицательной) (рис. 32 и 33).

Пусть М\ ж М2 - соответственно последние о,бщие точки этих полутраекторий с окружностью С (так что часть MiO полутраек-

тории Ll и часть МО полутраектории L2 уже не имеют общих точек с С, кроме Mi и М).

Рассмотрим область а, граница которой состоит из части М\0 полутраектории Li и части МО полутраекторип L2, точки О и той из дуг окружности С с концами Mi и М, на которой направление от точки Ml к М2 является движением против часовой стрелки на С.

Будем область а называть областью {сектором) между полутраекториями Ll и L2"). При этом: 1) область а между полутраекториями Ll и L2 будем называть гиперболической или сед-ловой областью {сектором) и обозначать через Ос, если через все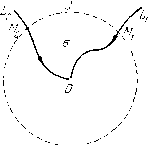

Рис. 32

Рис. 33

точки этой области проходят траектории, как при возрастании, так и при убывании t выходящие из а. В этом случае Li и L2 являются, очевидно, сепаратрисами состояния равновесия, причем одна из них стремится к О при t + оо, а другая - при - оо (см. рис. 27, где под L+ понимается полутраектория L2, а под L~ - полутраектория. Li). 2) Область а между полутраекториями Ll и L2 называется параболической или открытой узловой областью (сектором), если через все точки этой области, лежащие внутри некоторой достаточно малой окружности С {С лежит внутри С), проходят траектории, которые при - + 00 (f oo), не выходя из а, стремятся к состоянию равновесия О, а при убывании (возрастании) t выходят из а ).

Окружность с при такой терминологии не указывается; это находится в согласии с тем, что сказанное ниже относительно характера области о не зависит от окружности С, если только радиус этой окружности меньше некоторого определенного числа го. Порядок, в котором перечисляются траектории Ц и Lc- очевидно, не безразличен.

*) Если все полуграектории параболической области стремятся к состоянию равновесия при t-f-oo [t-00), то они, очевидно, являются о)-(а)-орбитно-устойчивылш. Однако среди них могут быть полутраектории особых траекторий, являюш;ихся а-((о)-орбитно-неустойчивыми.