Используя построенную вокруг сшитого фокуса функцию последования, нетрудно видеть, что, когда

bi + b* = 0, афО

(т. е. когда мы имеем простейший сложный фокус), прп измене-НШ1 коэффициентов bi и bi (так, чтобы выражение ai сделалось не равным нулю п надлежаш;его знака) из сложного сшитого фокуса рождается сшитый предельный цикл (и только один) той же устойчивости, что и сложный сшитый фокус.

Если при изменении коэффициентов Ъ\ и сшитый фокус из устойчивого делается неустойчивым, то здесь возможна та же смена качественных структур, что и рассмотренная в гл. 11, 13 при смене устойчивости фокуса аналитической системы.

Пусть теперь у рассматриваемого сложного (сшитого) фокуса первый не равный нулю коэффициент - аФО, где к> 2.

Тогда без труда можно установить, что в случае, когда коэффициенты а, аналитически зависят от параметров (это, очевидно, будет всегда, когда правые части сшиваемых динамических систем - аналитические функции параметров), то из такого фокуса может при сколь угодно малых изменениях параметров родиться не более к предельных циклов. То или другое число к предельных циклов рождаемся при том или другом характере зависимости коэффициентов а, {i < к) от параметров.

2. Сшитый нз обыкновенных траекторий «квазифокус» п рождение предельных циклов из такого фокуса [72]. Пусть линия сшивания есть х = 0 п в некоторой окрестности точки О {О, 0) определена сшитая система

dx/dt = Pi{x,y),

dy/dt = Qi{x,y),

dxldt=P2{x, у), dyldt = Q2{x,y),

Тогда О {О, 0) не является состоянием равновесия ни для одной из систем (8) и (9).

Нетрудно показать, что расположение траекторий в окрестности начала координат будет таким, как представлено на рпс. 197 (если <2i(0, 0)>0), или таким, как представлено на рис. 198 (<?i(0, 0)<0), если выполнены следуюгцие условия:

Pi(0, 0)=Р2(0, 0) = 0, (10);

W" (0,0),(0,0X0. (И)

Условие Pi (О, 0) = Р2(0, 0)=0 есть условие касания траекторий соответственно систем (8) и (9) оси а; = 0. Условие (11) может

быть получено, если для определения вогнутости интегральной кривой, предполагая ее заданной в виде x = f{y), подсчитать f" (у), пользуясь системой (8) или соответственно (9), записанными в виде одного уравнения dx/dy = Pi{x, y)/Qi{x, у), соответственно dx/dy = Р2{х, y)/Q2{x, у). Неподвижная точка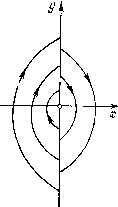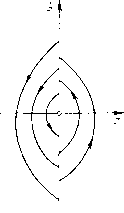

Рис. 197

Рис. 198

0(0, 0) (квазифокус) обладает свойствами, аналогичными фокусу.

Для исследования свойств и бифуркаций такого квазифокуса построим в его окрестности на линии сшивания а; = О функцию последования (точечное отображение), как и в случае настоящего сшитого фокуса (см. § 4, п. 1). Будем строить эту функцию последования из двух функций соответствия между положительной и отрицательной полуосью у: одной - по траекториям системы (8) и другой - по траекториям системы (9). Будем строить эти функции соответствия, используя общие интегралы систем (8) и (9), в окрестности точки 0(0, 0). Так как точка 0(0, 0) является неособой точкой для систем (8) и (9), и (по условию) каждая из этих систем определена в некоторой полной окрестности точки 0(0, 0), то в силу общих теорем (см. гл. 1) в окрестности этой точки (локально) существуют интегралы этих систем вида

Fi{x,y) = C, F2{x,y)=C,

где Fi{x, у) и F2{x, у)- аналитические функции.

Установим прежде всего некоторые элементарные свойства этпх интегралов в рассматриваемом нами случае. Так как мы имеем

Fi{x,y)Pi{x,y) +Fiy{x,y)Qi(x,y)0, t = 1, 2, (12)

то, в частности,

Fix(0,0)Pi(0,0) + F;0,0)i(0, 0) = 0, i=i,2. (13)

Но в силу иредиоложения Рг{0, 0)=0, .(О, 0)Ф О мы должны иметь

F-y(0, 0) = 0, i=l,2.

А тогда, очевидно, что Fix{0, 0)фО (так как точка О {О, 0) не является особой точкой систем (8) и (9) и не может, следовательно, быть особой точкой интегральных кривых, проходяш;их через эти точки). Так как (12) выполняется тождественно, то, продифференцировав его по t, мы также получим тождество

KPi + FlvQi) Pi + Pix {PixPi + PiyQi) +

+ [p"i-yPi + Qi + Fly {QlPi + QlyQi) = 0, i = 1, 2.

В частности, при x = у = О мы получаем в силу того, что Pi (О, 0) = О и F[y (О, 0) = О, cлeдyюиee выражение:

Fl (О, 0) Р-у (О, 0) Qi (О, 0) + F".y. (О, 0) Q] (О, 0) = 0.

Но так как (0,0)=О, Р[у{0,0)фО и Qi{0, 0)¥=0, то очевидно, что

V(0, 0)=0.

Таким образом, из сделанных нами предположений (10) и (И) вытекает условие на функции Fi{x, у):

F;,(0,0) = 0, /?;2(0,0)=0. (14)

При этих условиях мы будем строить функцию последования.

Для построения функции соответствия (согласно § 3 гл. 5) между положительной и отрицательной полуосью у введем на них параметры так, чтобы углы между траекторией и соответст-вyюпeй той и другой полуосью, на которых положительное направление есть направление возрастания параметра, были одного знака.

Такими параметрами, очевидно, будут у - и ва положительной и у = -V на отрицательной полуосях. Функции соответствия ио траекториям систем (8) и (9) могут быть заданы сле-дyюпими неявными уравнениями:

Fi{0, -vi)Fi{0, и), (15)

F2{0, -V2)= F2iO, и). (16)

Как мы видели (см. § 1 гл. 5), производная от функции ооответ-<;твия всегда положительна. Но неявные уравнения (15), (16)