так и происходить после него. Кривая L° не пересекает прямую Ol = О, на которой фокус меняет устойчивость, на отрезке между осью d и +-кривой (пересечение невозможно при f = о, так как Рф + Qv не меняет знак на Oi = О и, следовательно, невозможно и при малых y).

Последовательность качественных структур, переходящих одна в другую прп описанном изменении параметров, представлена на рис. 178 двумя возможными последовательностями грубых структур: 1-4, 6 или 1-3, 5, 6. Негрубые структуры, соответствующие бифуркационным значениям параметра, обозначены двумя цифрами, указывающими па грубые структуры, которые они разделяют. При движении вдоль •l-кpпвыx (о < A;i <(3/4)яу) структура 1 выпадает пз последовательности (Агкривые не пересекают кривую а32(1) = 0).

Обратимся к случаю d<0. Условие (4) выде.ляет на плоско-стп (Я, d) область, для точек которой в фазовом пространстве системы (1) есть устойчивый предельный цикл на верхнем полуцилиндре. При d < О состояние равновесия 0\ устойчивое. Качественная структура фазового пространства в этой областп будет такой, как на рпс. 178,4. Кривые к (для - (3/4) лу < А; < 0) соединяют областп пространства параметров, соответствующие структурам, представленным на рпс. 178, 4, 6. При возрастании Я вдоль А;-кривых точки Ра и Ръ на со- и а-сепаратрпсах седла на верхнем полуцилиндре (см. рис. 179) монотонно сближаются, сливаются при некотором значении Я = Яо(А:) (соответственно d = do{k)) и затем монотонно расходятся. Множество точек (Хо(к), do(k)), соответствующее негрубой бифуркационной структуре, для которой а- и ю-сепаратрисы седла образуют петлю на верхнем полуцилиндре, образует непрерывную кривую - продолжение L-кривоц в область d < 0. Через любую точку L проходит одна пз А;-кри-вых (-(3/4)яу <А;<0).

Седловая величина = (Р + Qy) = - Я (l 4- d Vi - у)

меняет знак в плоскости (Я, d) па прямой 1 + йУ1 -у = 0. Эта прямая пмеет лишь одну точку пересечения с /у-кривой (так как Z/+ не может иметь с А;-кривыми более одной точки пересечения).

Существует единственное значение к = ко, разделяющее А;-крп-вые на два класса: Агкривые (A;o<A;i<0), пересекающие L" прп О2<0 п Аг-кривые (-(3/4) л < А;2 < fto), пересекающие при 02 > 0. При малых Я осуществляется структура, представленная на рпс. 178, 4. При возрастании Я вдоль А;1-крпвых предельный цикл опускается, а сепаратрисы на верхнем полуцилиндре сближаются.

При переходе через значение Я, соответствующее пересечению кривых ki и L"*", возникает и затем разрушается петля сепаратрисы на верхнем полуцилиндре, к которой стягивается устойчивый

предельный цикл (так как седловая величина Ог < 0). При дальнейшем изменении параметров вдоль А;1-кривых изменения качественной структуры не происходит. Последовательность качественных структур при возрастании Я вдоль А;1-кривых представлена на рис. 178, 4, 178, 4-6, 178, 6.

При возрастании X вдоль А;2-кривых предельный цпкл опускается и сепаратрисы на верхнем полуцилиндре сближаются, но при переходе через значение Я, соответствуюш;ее пересечению кривых к2 и при разрушении петли сепаратрисы появляется неустойчивый предельный цикл на верхнем полуцилиндре (устойчивый предельный цикл не может стянуться к петле сепаратрисы, так как седловая величина 02 > 0) и возникает структура, представленная на рис. 178,7, с двумя предельными циклами, охватываюш;ими верхний полуцилиндр.

Прп дальнейшем возрастании параметра % вдоль А;2-кривых предельные циклы монотонно сближаются. Так как для структуры на рис. 178,6 предельных циклов нет, то суш;ествует на каждой •2-кpивoй точка с координатами Я++(А;), d+"(A;), для которой устойчивый и неустойчивый предельные циклы сливаются, образуя полуустойчивый предельный цикл. Соответствуюш;ая негрубая бифуркационная структура представлена на рис. 178,7-6. Множество точек (Х"+(А;), d*+(ft)) образует непре-

рывную

кривую, пересекаюш;уюся с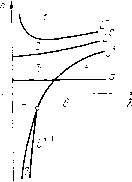

Рис. 180

каждой пз А;2-крпвых в одной точке справа от L+-KpnBon и начинающуюся в точке пересечения Ь+-кривой с прямой 02 == = 0 (рис. 180).

Последовательность качественных структур при возрастании % вдоль А;2-кри-вых представлена на рис. 178, f; 178, J- 7; 178,7; 178,7-6 и 178,6.

Разбиение пространства параметров %, d при малых Y представлено на рис. 180 цифрами 1-7 отмечены области в пространстве параметров, соответствующие

грубым структурам в фазовом пространстве, помеченным теми же цифрами на рис. 178. Негрубые структуры на рис. 178, помеченные двумя цифрами, соответствуют бифуркационным кривым рис. 180, разделяющим соответствующие области.

Замечание. Определение ""-кривой опирается на существование ""-кривой, доказанное с привлечением метода малого параметра и, следовательно, для области фазового пространства, ограниченной по координате у. Для двойных циклов, расположенных в далеких частях фазового цилиндра, нужно рассматривать продолжение Ь-кривой. Асимптотическое поведение продолжения """"-кривой дано в приложении II.

5. Поведение бифуркационных кривых в зависимости от f. Другие возможные бифуркации. Проследим за изменениями в фазовом пространстве и поведением бифуркационных кривых при переходе от малых положительных значений ч к немалым в интервале При возрастании состояния равновесия

Ol и О2 сближаются. Поле направлений на нижнем п верхнем полуцилиндрах монотонно поворачивается соответственно по и против часовой стрелки, и при этом устойчивые предельные циклы на верхнем и нижнем полуцилиндрах поднимаются. Если устойчивый предельный цикл на верхнем полуцилиндре существует для некоторого Yoi то он будет существовать и для всех > Yo. Если для некоторого Yo существует петля на нижнем или верхнем полуцилиндрах, то при возрастании y петля снизу разрушается без возникновения предельного цикла, а петля сверху - с возникновением устойчивого предельного цикла. Точки /у"-кривой, разделяющей области i и 2 на рпс. 180, при возрастании Y становятся внутренними точками области 2. При воз-растанип y точки L-кривой становятся внутренними точками областей 3 ш 4, а. точки L-кривой - внутренними точками областей 4 ж 7 (либо принадлежат их границе). Кривая L, начп-пающаяся в точке пересечения L* с прямой 1 + йУ1 -Y = 0, не существует выше прямой (предположение о существованип таких точек приводит к необходимости существования для двух значенпй Yi и Yo точек пересечения кривых L*"*"(Yi) и Ь++("(о), что невозможно из-за монотонности поворота поля на полуцилиндре при монотонном изменении y)> и поэтому условие 1 + + йУ1 -Y<0, может служить оценкой областп существования структуры разбиения фазового цилиндра с двумя предельными циклами на верхнем полуцилиндре, представленной на рнс. 178, 7. Область 7 пространства параметров, соответствующая структуре па рис. 178, 7, с возрастанием y опускается.

При возрастании Y до значения {= I состояния равновесия Ol и Ог сливаются, образуя сложную особую точку седло-узел, а области 1-3, 5 ж 7 рис. 180 уходят в бесконечность. На плоскости ед1шственной бифуркационной кривой будет L-кривая (ее существование следует из рассуждений, аналогичных рассуждениям для случая малых , опирающихся на существование при Y = 1 некоторой окрестности оси d, для точек которой есть устойчивый предельный цикл на верхнем полуцилиндре). Пространство параметров и структуры разбиения фазового пространства изображены на рис. 181.

При Y > 1 существует единственная структура разбиения фазового пространства на траектории. Все траектории накручиваются на устойчивый предельный цикл на верхнем полуцилиндре (рпс. 182). При возрастании y от значения Y = 1 при К ж d, взятых пз области 1 рис. 181, исчезает состояние равновесия седло-