удовлетворяется тождественно при подстановке у = к,х. Действительно, мы имеем

ki {ах + bkiX - х{х + klx)) = сх + dkiX - kiX {х + кх),

X {Ьк\ + (a - d)ki - c) = О,

так как выражение в скобках равно нулю (h есть корень уравнения (4)). Характер состояния равновесия в начале координат легко может быть определен по корням соответствующего характеристического уравнения. Для исследования остальных состоя-нпй равновесия достаточно ограничиться рассмотрением каких-либо двух, не лежащих одновременно на одной и той же прямой у = к,х, так как векторное поле, определяемое системой (3), симметрично относительно начала координат. (Система (3) не мепяется при замене х на -х и г/ на -у.) Определение их характера путем вычисления характеристических корней очень громоздко, и это можно сделать проще, воспользовавшись теорией индекса Пуанкаре.

Так как при D > О все состояния равновесия простые, и при изменении знака D, когда корни ki и /сг делаются мнимыми, исчезают (кроме (О, 0)), то сумма их индексов должна равняться нулю. Кроме того, ни одно из них не может быть фокусом, так как через них проходят интегральные прямые у = kiX. Отсюда заключаем, что одно из них - седло, другое - узел.

Когда D = О, эти точки сливаются в двойную точку - седло-узел (если при этом АФО).

В случае А = О две симметричные точки сливаются с особой точкой в начале координат в одну и образуют особую точку высшего порядка. Заметив, что при А > О индекс особой точки в начале координат равен а при А<0 равен -1, заключаем отсюда, что сумма индексов особых точек, слившихся с началом, равна -2, т. е. эти особые точки-седла, и сложная особая точка имеет характер седла, а оставшиеся две - узлы.

В случае, когда

D{a-d) + Abc<0,

система имеет в начале координат единственную особую точку типа фокус. Постараемся выяснить наличие предельных циклов. Выберем- в качестве топографической системы семейство окружностей

а;2 + г/2 = (g

Тогда контактная кривая (т. е. кривая, где окружности (6) касаются траектории системы (3)) будет иметь вид

cx-\-dy - y (х + у) х

ахЪу - х {х -\-у)~ у

F{x, y)=ax + {b + с)ху + dy-{x + у)= 0. В полярных координатах

2р2 = я + d + (а - d) cos 2ф + (& + с) sin 2ф.

Радиусы R\ и 7?2 крайних кругов, касающихся кривой контакта,

определяются из условия dp/dtp = О, которое дает tg 2ф = 1 .

Отсюда находим радиусы крайних кругов топографической системы, касающихся контактной кривой:

Р a + d± Y{a-df + ib + e) 2 =---.

Предельный цикл лежит в кольцевой области между этими кругами, R\ и 7?2 будут оба положительными, если {а + d)> >{а - d) +{Ь + с), или Aad - (Ь + с)> 0. Последнее условие совпадает с условием, при котором кривая контактов имеет в начале координат изолированную точку:

FxxFyy - {FlyY = Ш -(b + > 0.

Если это условие не выполнено, кривая контактов проходит через начало координат, а величина R] становится отрицательной, и можно лишь утверждать, что предельный цикл (еслп он существует) располагается внутри окружности радиуса i?2. Нетрудно доказать, что предельный цикл единствен. Воспользуемся с этой целью критерием Дюлака для кольцевой области (см. гл. 6). Очевидно, что функции

Х{х, у)=ах + Ьу - х{х + у), Y{x, у)= сх + dy - у{х + у)

by-c.r+ia-d)xy

удовлетворяют условиям теоремы Дюлака для кольцевой области (см. гл. 6), так как в этом случае F{x, у) дифференцируема в любой кольцевой области G, окружающей начало координат. Легко проверить, что

В{X, у) = (XF) + ±- (YF) = -2(хЧЛ

9у > Ъу - сх + {а - d) ху

не меняет знака в области G. Таким образом, цикл один.

Доказанная единственность предельного цикла позволяет утверждать, что при смене устойчивости особой точки в начале координат предельный цикл стягивается в особую точку.

В самом деле, в противном случае должно было бы существовать четное число предельных циклов. Отсюда же следует, что для я + d < О предельных циклов нет.

На рис. 127 и 128 даны картины разбиения сферы на траектории для случая одной особой точки: рис. 127 - для D<0, a + d>0; рис. 128 - для А > О, а + d < 0.

Взаиморасположение различных областей значений параметров системы (разбиение пространства коэффициентов системы) может быть дано в очень удобной и наглядной форме. Заметим с этой целью, что заменой t = x/d, х = Уй, у = Ут] система (2)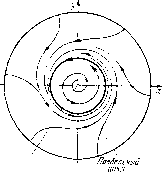

Неустойчивый фокус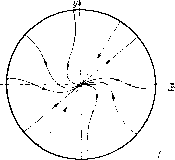

Рис. 127

Устойчивый иеп Рис. 128

может быть приведена к виду, где d = 1 (для d>0). Тогда пространство коэффициентов может быть реализовано в виде плоскости (я, Ъс). На рис. 129 изображены кривые Д = О, А = О, а + d = О, разбивающие плоскость на области, соответствующие различным случаям разбиения сферы на траектории. Области 7 (рис. 129) соответствует разбиение сферы на траектории, изображенное на рис. 130; области 77 соответствует рис. 131 и т. д. Точкам плоскости, лежащим на прямой А = О, соответствуют бифуркационные значения параметра, при которых начало координат является особой точкой высокого порядка. Качественная картина на сфере эквивалентна в этом случае либо рис. 131 {a-\-d> >0), либо рис. 128 (я-fdO). Штриховкой на рис. 129 покрыта область, для которой существует предельный цикл. Случай 7) = О, А > О изображен на рис. 132. Пример 3 [4].

dxjdt = -ау + X (I - х" - у) = Р,

dy/dt = А + ах + у(1 - х - у) Q.

Рис. 129