странства, возможно, различающиеся лишь четным числом предельных циклов. Такая постановка задачи нередко бывает полезной, так как позволяет расширить класс характеристик, расширяет возможности разумного выбора аппроксимации и тем самым иногда возможности получения практически полного знания всех важнейших особенностей в работе устройства в зависимости от параметров. В то же время такой подход оставляет в стороне часто неразрешимую задачу прослеживания бифуркаций, связанных с двойным циклом. Мы проведем сравнительное рассмотрение качественной структуры при разных аппроксимациях на ряде задач. В качестве первой из этих задач возьмем классическую задачу динамики полета, которая в случае аналитической характеристики была рассмотрена в гл. 16. Именно, рассматривалась система

йф/dt = р - cos ц) = Р, йрМ==2р(Я-рр-8тф)=(?.

Выбор этой задачи обусловился тем, что в исходной системе возможен широкий набор бифуркаций (осуществляются все типы бифуркаций первой степени негрубости) и удалось строго установить структуру разбиения пространства параметров как для исходной системы (что до сих пор не было сделано), так и для аппроксимирующих систем. Здесь возникают различия в структуре разбиения пространства параметров и фазового пространства, позволяющие оцепить влияние аппроксимаций на структуры разбиения и обнаружить, в частности, важную роль, которую играет «седловая величина» (см. гл. 9). Сохранение количественной близости характеристик ие оказалось обязательным для сохранения качественной структуры разбиения фазового пространства и пространства параметров системы. Использование седловой величины при качественном исследовании сшитых систем опирается на возможность перенесения утверждений, касающихся условий устойчивости петли сепаратрисы (см. гл. 9) и рождения от нее предельных циклов, на неаналитические системы (см. гл. 17), содержащие петлю, в состав которой входит аналитическое седло.

§ I. Рассмотрение системы (2) при аппроксимациях пилообразными функциями. Примем такую аппроксимацию (рис. 229);

( 2/л)ф-2, [-Л,-л/2], sin ф ~ «2 = (2/л)ф, (- л/2, л/21,

(-2/л)ф+2, [л/2, л];

(2/л)ф+ 1, [-Л, 0], С08ф~С2= ( 2/я)-ф + 1, [О, л].

Состояния равновесия на полосе -я ф я будут Oi(-n/2, 0), 02(я/2, 0), Оз{фз, Рз), р*), где

Фз =

я (Я, - ц)

Рз =

2(1 + ц) fs- 1

Ol - сшитое седло, О2 - сшитый неустойчивый узел, Оз - узел или фокус, Oi - седло. В пространстве параметров на прямой Я - р, = О сливаются точки О3 и Oi, на прямой Я = 1 - точки 4 и О2.

1. Структура разбиения фазового пространства для точки = М=1 При Я = р==1 на интервале Офя/2 совпадают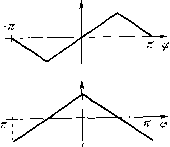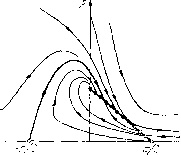

Рис. 229

Рис. 230

изоклины вертикальных и горизонтальных наклонов, и возника-«т структура разбиения фазового пространства с отрезком покоя «а интервале О ф п/2. Интегральными кривыми, по которым -движутся изображающие точки на интервале О < ф < я/2, будут экспоненты; р = 1 - 2я"ф (О < ф я/2) - отрезок покоя, устойчивый на интервале 0<ф<(я -1)/2 и неустойчивый на интервале (я - 1)/2 < ф < я/2. В точке ((я - 1)/2, я") интегральная кривая р = я~е"~" касается отрезка покоя и при ф = О попадает в область выше максимума изоклины горизонтальных наклонов (я~е"~ > 2) и уходит в бесконечность. Предельных циклов нет. Все траектории при t + оо идут к устойчивой части отрезка покоя. Структура разбиения фазового пространства в окрестности отрезка покоя представлена на рис. 230.

2. Структура разбиения на прямой Я.= (х. При возрастании Я и р от значения Л = р, = 1 вдоль прямой отрезок покоя распадается, и на его концах возникают особые точки: Оз4(0, 1) - сшитая из фокуса и седла и 02(л/2, 0)- сшитый узел (неустойчивый). Изоклина горизонтальных наклонов располагается на интервале О < ф < л/2 выше изоклины вертикальных наклонов, и сепаратриса седла Oi, заканчивавшаяся при Я = (i = 1 на устойчивом куске отрезка покоя, превращается в траекторию, накручивающуюся на предельный цикл, охватывающий цилиндр (бес-

конечность неустойчива). Устойчивый предельный цикл появляется из траектории, примьшающей к отрезку покоя, и куска отрезка покоя.

При возрастании Я и р вдоль прямой седло-фокус О34 превращается при р =(1 + 2Уп)/п = р* в седло-узел с устойчивой узловой областью. Обе со-сепаратрисы сшитого седло-узла для ji, близких к р*, должны выходить из узла 0%. Для больших Лиц предельных циклов нет, так как со-сепаратриса, входящая в седло-узел, имеет всюду отрицательный наклон. Справедливость зтого следует из того, что если взять точку (фо, т1о> 1) на со-сепарат-рисе, то при достаточно больших р координата tjo па прямой Ф = фо будет больше максимума изоклины горизонтальных наклонов (Я.-1- 1)/р., так как в области р> 1 векторное поле поворачивается по часовой стрелке при возрастании р вдоль прямой и при зтом Tjo растет, а (Я4-1)/р->-1.

Качественные структуры, последовательно переходящие одна в другую при возрастании р и Л вдоль прямой Л = р, будут эквивалентны некоторым представленным на рис. 168 гл. 16, § 4. Для любого р из интервала О < р < р* структура разбиения фазового пространства эквивалентна изображенной на рис. 168, П-1П, для р* < р < pi - на рис. 168, для pi < р < р2 - на

рис. 168, IY. Для р2 < р < °° расположение сепаратрис будет таким, как на рис. 168, F.

3. Структура разбиения на полупрямой 11 = я(Я-1)-1-1>1. При возрастании Л и р от значений Л = р = 1 вдоль полупрямой кусок изоклины на интервале О < ф < п/2 поворачивается вокруг точки ((я - 1)/2, п~), и отрезок покоя распадается с возникновением трех особых точек: 0% (фз, рз) - устойчивый фокус или узел, 04((я - 1)/2, п~)- седло с направлениями для сепаратрис, определяемыми уравнением v?\i + 2п (1 -Ь р) /с -Ь 4 = О, я 02(я/2, 0)- сшитый узел (неустойчивый). Контактная кривая с кривыми вырожденной системы (р = Л = 1) при изменении параметров вдоль прямой будет р = п~ и, следовательно, всегда проходит через седло. Векторное поле в области р > 1 поворачивается при возрастании р по часовой стрелке, и поэтому со-сепаратриса, идущая в седло по направлению к < -2я~, не может пересекать интегральную кривую р = я~е"~~ вырожденной системы, касающуюся отрезка покоя как раз в той точке, в которой при р > 1 возникает седло, и входящую в седло по направлению к =-2л~К Сепаратриса пересекает ось ф = 0 в точке р* > > я-е"" > 2 и входит в область выше максимума изоклины горизонтальных наклонов. Предельных циклов, охватывающих цилиндр, нет при любых значениях Л и р на рассматриваемой полупрямой. Структура разбиения фазового пространства для всех точек зтой полупрямой будет одинакова и эквивалентна изображенной на рис. 169, S (§ 4 гл. 16).