(1 + --р)]г/сгф + (1---р)г/ф"

Здесь Li и 2 -части интегральпой кривой системы (1), при

р = 0 проходящей через точку Р{-л/2, уЧ) {О<:у1< У/), расположенные соответственно в интервалах -п < ф -л/2, -л/2 < ф 0.

Уравнения кривых Li и L2 имеют вид

4 (Ф±£)! = Й,, (L,)

Из выражения (4) следует, что при (1 - 2р/л) (1 + 2р/л)> Q уравнение F {yf) = О не имеет действительных корней. Пусть 1 - 2р/л < 0. Легко видеть, что

з(Й1) = 2г)1(М-4яуо. кЮ-РЛК), biK)--2M. При значениях hi, удовлетворяющих условию (5), имеем ih) < О, 13з (- л/4) > О, Иш {hj) = - 00,

% (- л/4) = - 2%д Ylq2 (1 - 2Р/Л) л4 > О, lim трз (Ai) = V 2 л(р - 2 - л/2).

Отсюда находим, что при 1 - 2р/л < О, р - 2 - л/2 < О существует единственный устойчивый предельный цикл, охватывающий состояние равновесия. Аналогично можно показать, что при 1 -2р/л>0 система (1) не имеет циклов, охватывающих состояние равновесия.

Для выяснения качественной картины фазовых траекторий заметим, что состояние равновесия Oi (руол/2, 0) будет устойчивым фокусом при рЯо(1 - 2р/л)>0 и неустойчивым фокусом при р;.о(1-2р/л)<0.

На рис. 199 приведено разбиение пространства параметров Yo, Яо и р на области, точкам которых соответствует определенная качественная картина фазовых траекторий.

25 н. Н. Баутин, Е. А. Леонтович

Находим, наконец, предельные циклы, охватывающие состояние равновесия.

Тогда, применяя теорему 1 § 5 гл. 12, будем иметь

в области 1:

4о + ЯоУл/2(р-2-л/2)<0, 1 + 2р/я<0,

tfi(A) = 0, Mh)>0,

система (1) пмеет два предельных цикла, охватывающих цилиндр в верхнем фазовом полупространстве. Верхний цикл устойчивый, нижний неустойчивый.

В области 2: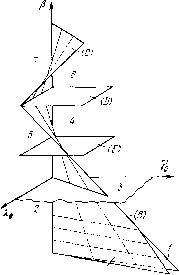

То>0, 40+A,oVя/2(p-2--я/2)<0, 1-2р/я>0, [{h) = 0, ij)i(/i)<0,

система (1) не имеет предельных циклов.

В области 3:

Рис. 199 В области 4:

Яо>0, 4то + ЯоУя/2(р-2-

-я/2>0, 1-2р/л>0,

система (1) имеет один устойчивый цикл, охватывающий цилиндр в верхнем фазовом полупространстве.

Яо>0, 4-(о + ХоГя/2(р-2-л/2)>0,

1 - 2р/я < О, р - 2 - я/2 < О,

еистема (1) имеет один устойчивый предельный цикл, охватывающий состояние равновесия, и один устойчивый предельный цикл, охватывающий цилиндр в верхнем фазовом полупро-етранстве.

В области 5:

Yo>0, Яо>0, 4о + ЯоГл/2(р-2-л/2)<0, 1-2р/л<0,

еистема (1) имеет один устойчивый предельный цикл, охватывающий состояние равновесия. В области 6:

р-2-я/2>0, Яо>0, Yo>0,

- 4yo + ЯоЫ2 (р - 2 - я/2) < 0;

еистема имеет один устойчивый предельный цикл в верхнем полупространстве.

В области 7:

Yo>0, Яо>0, -4то + ЯоГя/2(р-2-я/2)>0,

система (1) имеет два устойчивых цикла, охватываюш;их цилиндр. Один из них расположен в нижнем, а другой в верхнем фазовом полупространстве.

Качественные картины фазовых траекторий для перечисленных областей изображены на рис. 200.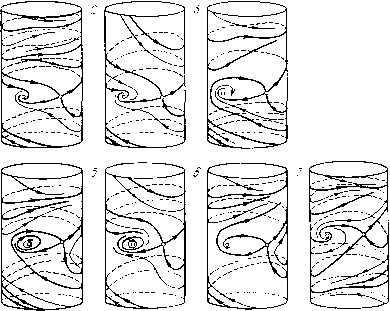

Рис. 200

Рассмотрим качественные картины фазовых траекторий на бифуркационных поверхностях.

На поверхности {А), определяемой соотношениями

система имеет полуустойчивый и предельный цикл, охватывающий цилиндр в верхнем фазовом полупространстве (рис. 201,/.2).

На поверхностях {В) и (С) соответственно (рис. 201, 1.3 и 201, 6.7)

4о + ЯоУя/2(р-2-я/2) = 0,