Для разомкнутой системы можно записать:

Хц Хц

A, ,-B„[kD, 1 А, „ Aii-iC] I Ац-п BhCj LCn

-B„kD„ О

Ah -- LCh

Auy +

Bmll

Me. (5.1)

Коэффициенты регулятора определяются по структуре, включающей в себя невосстанавливаемую часть объекта и модель соответственно с векторами выходных координат Х] и Хц (при L = 0). Поскольку в рассматриваемом случае (7mi + -f Т„з + + 7„4)/Г„1 » 1, влиянием связи с передаточной матрицей Aj.u на стадии определения коэффициентов можно пренебречь. Тогда

Если по-прежнему считать, что токовый контур описывается звеном второго порядка (2.16), то при Xj = col UiXaXg], где = = Ai„; Xg = A coi, и Xji = col {х1„х„ХзаХ4н], где х-хп - выходные координаты модели (а при L-O - выходные координаты наблюдателя), входящие в выражения (5.2), матрицы имеют вид:

с1ы

C, = [0 0 1]; Г 2

к = [0 О fei Й2 3 4 ky< Di =

Матрица Dj имеет размер 7 X 3, а - 7x4, через I3 н I4 обозначены единичные матрицы 3-го и 4-го порядка.

Начала Ввод

п-5-

])=detA

Hemes

гг7-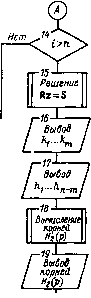

2(Й-V

(Конец)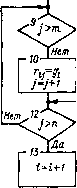

линома а (р), образующие

im/Ji • • . /Z„ mJ, могут быТЬ

матричного уравнения Rz = S, рицы R определяются как Гц =

Рис. 5.5. Алгоритм определения коэффициентов регулятора скоростной подсистемы

Аналогично изложенному в § 2.3 применительно к двухмассовой системе, задача сводится к определению матрицы регулятора к, при реализации которой обеспечивалось бы желаемое распределение управляемых корней при незначительном влиянии неуправляемых.

Для ее решения разработан алгоритм расчета коэффициентов регулятора и значений неуправляемых корней в системе /г-го порядка при т связей по координатам объекта Чтобы воспользоваться им, надо выражения (5.2) записать в виде:

x = AoX+B„u; u = Auy -кх,

где первые т элементов вектора координат X ирпользуются для введения связей при к = [/fe . . .

. . .01. Характеристический полином замкнутой системы представляется как Я° (р) == = Я? (р) Н, {р) при Я? (р) =

+ . . . +щ\Н2{р)= -f + hi уэ"-"- + /j2P"-«-2 +. . . -f

+ hnm- Если матричную передаточную функцию объекта х(р)/и(р) = [р1-Ао1-1 В„ записать в виде X {р)1и (р) =g {р)1 det [р\-АоЬ то коэффициенты регулятора и коэффициенты по-вектор-столбец z = col {1 . . . найдены в результате решения в котором элементы [п X /г)-мат-

gi ipi) при / < т; ги= Hi (pi) pf

при / > т, где gi {pi) - элемент матрицы-столбца g {р), номер которого равен /, pi - число, образованное как р; р + dp; + \-2dp . . . , где d - шаг варьирования pi. Элементы матрицы-столбца S вычисляются как s, = (pi)"" - det [pi I-Ао). При известных коэффициентах . . . hm определяются корни полинома Hiip).

Структурная схема алгоритма приведена на рис. 5.5.

Расчет производится для ряда значений ©о, после чего выбирается такое, при котором неуправляемые корни будут располагаться вне окружности с радиусом, в два раза превышающим радиус окружности управляемых корней.

3. При четырехмассовой разветвленной модели объекта (см. табл. 4.1) с учетом демпфирования матрицы, входящие в уравнение (5.1), имеют вид:

i-i -

И-11 =

Ап-1

с21

о о о