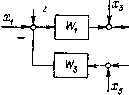Рис. 1.12. Инверсия пути S)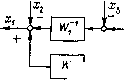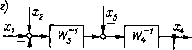

Рис. 1.13. Инверсия контура

В качестве самостоятельного упражнения читателю предлагается определить передаточную функцию между переменными х и у для структурной схемы, изображенной на рис. 1.11,6, двумя способами: с помощью структурных преобразований (при кажущейся простоте схемы они будут довольно сложными) и по правилу Мейсона. В последнем случае необходимо обратить особое внимание на то, что между переменными х я у имеются четыре пути.

Инверсия пути и контура. Одним из видов структурно-топологических преобразований является операция инверсии. Инверсию применяют, главным образом, для приведения структурных схем к виду, удобному для аналогового и цифрового моделирования, в результате устранения дифференцирующих звеньев.

Основное правило инверсии состоит в том, что при инверсии направления любого пути между двумя переменными структурной

схемы его передача становится обратной, а знаки всех сигналов, алгебраически суммирующихся иа инвертируемом пути, изме!1Я1()гся на противоположные.

Эго легко доказывается на примере схемы рис. 1.12, а, соответствующей уравнению у = W+ W-x. + It.j-Vy. Измекии па-правление пути от Хз к (/ на обратное с учетом сформулированного выше правила инверсии, получим структурную схему рис, 1,12, 6. что соответствует решению исходного уравнения отиосительио переменной х: х = WT {y-WiX-Wх)- В этом и состоит математическая трактовка операции инверсии пути, которая, таким образом, представляет собой не что иное, как графическое решение системы относительно другой переменной.

Из правила инверсии пути, как следствие, вытекает правило инверсии контура. Рассмотрим контур, изображенный иа рис. 1.13, а. Применив правило инверсии к пути между переменными Хх и Xi, получим схему, показанную на рис. 1,13, б. Проип-вертируем теперь путь от Xi к х, проходящий через обратную связь, В результате получим схему, изображенную на рис. 1,13, в, на которой замкнутый контур теперь имеет обратное направление. Сравнение полученной схемы с исходной позволяет сфор.мулиро-вать следующее правило инверсии контура.

При инверсии направления любого замкнутого контура передачи прямого и обратного каналов заменяют на обратные с проти-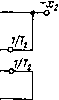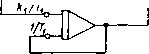

JiL.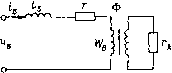

) i. is

1/4ф

h 4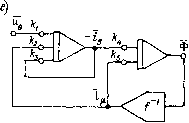

Рис. 1,15. Приведение нелинейной детализированной схемы к виду, удобному для моделирования на АВ.М: а - электрическая схема нелинейной электромагнитной цепи; б - схема замещения; в - детализированная структурная схема; г - результат инверсии контура; д - окончательный результат преобразования; е - схема набора иа АВМ

воположным знаком (замену знаков производят в узле сравнения). Знаки всех внешних воздействий, подходящих к контуру в любой точке, за исключением узла сравнения, также меняют на противоположные.

Если перерисовать последнюю схему так, как показано иа рис. 1.13, г, то полученный выше результат можно сформулировать иначе: в замкнутом контуре передачи прямого канала и обратной связи можно поменять местами, за.менив их на обратные значения и изменив на противоположные знаки подходящих к контуру внешних воздействий (за исключением сигналов, сум.мирующихся на узле сравнения).