йозможность измерять только ток якоря двигателя и его скорость, to для восстановления вектора состояния механизма соИшМгШа! может быть построен наблюдатель, для которого ток является сигналом управления (у = Ai), а ошибка восстановления определяется по скорости двигателя уи - ©i-©i, где © - восстановленная скорость двигателя. По-прежнему полагая, что условия пренебрежения обратной связью по ЭДС двигателя выполняются и токовый контур можно приближенно считать звеном, настроенным на оптимум по модулю, надо рассматривать объект с вектором состояния

= С01 \ХхХ2\Х.зХЧ\,

где Jfi -- выход первого интегратора в звене второго порядка, аппроксимирующее контур тока, не имеет физического смысла; jfj, = Aw, Хз - Д©1; Xi = АМаи х = А©2. Матрицы элементов структурной схемы на рис. 2.21 для этого случая приведены в описании формулы (2.18). Кроме того, Сц = П О 0], матрица D размером 5x2 - нулевая, Dn - имеет вид

D„ =

ГО О

о о о

1 о о

а матрица регулятора есть к == [00 iasl.

Структура замкнутой через наблюдатель системы показана на •рис. 2.22 (канал, изображенный штриховой линией, пока не рас- сматривается). Поскольку ошибка восстановления представляет

собой скаляр, матрица коэффициентов наблюдателя имеет вид

L= col UiiliJaA- Тогда

pl -(Aii !i -LC„):

P+ln

и характеристический полином (2.43) записывается как

I П Tui ) п V т,, г„, )

где Ту определяется формулой (2.8).

S-SOlb.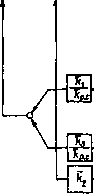

Релятор

Объект

Наёлюдателб

TImI 43-

Модель

Рис. 2.22. Система, замкнутая через наблюдатель, управляемый током якоря

Выбирая стандартный полином, например, полином, соответствующий распределению Баттерворта

Яв (р) = р+ 2щнр + 2шонР + ©Он

и приравнивая коэффициенты при одинаковых степенях р, можно получить выражения для коэффициентов наблюдателя:

21

1ш = 2-

(2.44)

где ©он - среднегеометрический корень, значение которого целесообразно выбрать так, чтобы быстродействие наблюдателя было выше быстродействия системы, за.мыкаемой через наблюдатель.

Коэффициенты наблюдателя имеют размерность частоты. На рис. 2.22 в отличие от рис. 2.21 интеграторы модели имеют постоянные времени Т; Td 72- Поэтому коэффициенты подаваемых иа

интеграторы связей наблюдателя представляют собой произведени я соответствующих коэффициентов и постоянных времени. Как было сказано выше, коэффициенты регулятора к; к и к могут выбираться так же, как при замыкании по непосредственно измеренным скоростям двигателя и ИО и упругому моменту, в частности, по формулам (2.24), а если предусматривается введение интегратора в закон регулирования, то по формулам (2.27).

Поскольку скорость двигателя измеряется непосредственно, на рис. 2.22 обратная связь с коэффициентом введена как связь по напряжению тахогенератора. Отметим, что при ограничении входного сигнала на регуляторе тока в результате ограничения выходного напряжения блока ограничения БО, действие обратных связей прекращается и вследствие наличия упругости могут возникнуть колебания скорости двигателя и исполнительного органа. Такой режим в процессе нормальной эксплуатации нужно исключить. Это может быть достигнуто при использовании задат-чика интенсивности на входе системы.

Описанный наблюдатель не обеспечивает точного воспроизведения вектора Хц, если на объект действует возмущение АМс. Существуют способы построения наблюдателей, использование которых позволяет получить точную оценку вектора состояния и в этом случае. Для этого необходимо, чтобы возмущающее воздействие могло быть идентифицировано и описано системой дифференциальных уравнений. Однако в большинстве случаев возмущение имеет произвольный характер и его математическое описание неизвестно. Тогда может быть поставлена задача точного восстановления координат лишь в установившемся режиме, когда Мс = const, т. е. АМс = 0. В переходных же процессах, связанных с изменением нагрузки, наблюдатель будет восстанавливать координаты системы и момент с ошибкой. Но и в этом случае наблюдатель будет восстанавливать вектор состояния с меньшей погрешностью. Связь, с помощью которой осуществляется восстановление Мс в статике, показана на рис. 2.22 штриховой линией. Восстановление Мс осуществляется в результате интегрирования ошибки восстановления скорости двигателя при действии момента нагрузки на ИО.

В этом случае рассматривается расширенный объект, порядок которого повышается на единицу, так как момент нагрузки рассматривается как одна из координат = АМс при 0. Для такого объекта на основании (2.18) можно записать

= Aij iCiXi + Ац 11Хп + В„,м,

Au-AxiF- О О оА?,; L mi j