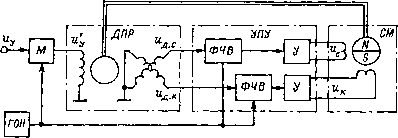Рис. 8.1. Функциональная схема бесконтактного моментного привода

трансформатора (СКВТ), работающего в амплитудном режиме, и двухканального усилительно-преобразовательного устройства УПУ, содержащего два фазочувствительных выпрямителя ФЧВ и два усилителя мощности У. Как статорные обмотки СМ, так и квадратурные обмотки ДПР сдвинуты относительно друг друга на 90 эл. град. В качестве ДПР в БМП обычно применяется бесконтактный СКВТ - редуктосин серии ВТ с тем же, что и в СМ, числом пар полюсов.

Управляющее напряжение постоянного тока «у модулятором М преобразуется в напряжение иу с частотой 0,4-10 кГц (опорное напряжение для модулятора и обоих ФЧВ вырабатывается генератором опорного напряжения ГОН). Последнее поступает на первичную обмотку (возбуждения) ДПР. Напряжения Ыд.с и Ыд.к, снимаемые с вторичных, синусной и косинусной, обмоток ДПР, в УПУ освобождаются от несущей частоты и усиливаются, после чего подаются на соответствующие фазы статорной обмотки СМ в виде напряжений Uc и Ык. Поскольку эти напряжения являются гармоническими функциями угла поворота ротора ДПР, то пространственная ориентация вектора МДС статора СМ полностью определяется угловым положением ротора ДПР. В БМДПТ ротор ДПР жестко связан с ротором СМ (см. рис. 8.1) и рдзвернут по отнощению к нему так, чтобы угол между векторами МДС статора и ротора СМ составлял 90 эл. град. Тем самым обеспечивается максимум значения электромагнитного момента и его независимость от угла поворота двигателя. Благодаря наличию указанной внутренней механической обратной связи двигатель утрачивает исходные свойства синхронной машины и по своим динамическим и статическим характеристикам становится подобным двигателю постоянного тока, являясь, по существу, обращенным вариантом последнего.

Вопросы математического описания бесконтактного электропривода в литературе рассматриваются почти исключительно в применении к задачам расчета параметров и статических характери-

стик БМДПТ [1, 87]. В то же время до сих пор почти не уделялось внимания построению математической модели бесконтактного двигателя, пригодной для исследования динамики и синтеза систем управления с БМП.

Различают два типа математических моделей БМП:

а) математическая модель, построенная в неподвижной (естественной) системе координат, связанной с осями а и b фаз статорной обмотки синхронной машины (см., например, работу [35]);

б) математическая модель во вращающейся системе координатных осей dug, связанной с ротором синхронной машины [87, 33].

Модель в естественной системе координат наиболее полно и точно характеризует специфику «электронного» двигателя, она наглядна, содержит реальные физические величины и пригодна для исследования процессов, происходящих в приводе, и анализа его характеристик. Но такая модель обладает и серьезным недостатком: она довольно громоздка и содержит параметры, являющиеся нелинейными функциями угла поворота ротора; это затрудняет, а чаще делает вообще невозможным восстановление недоступных непосредственному измерению переменных состояния электромеханических систем с БМП.

Математическая модель во вращающейся системе координат удобна тем, что ее параметры постоянны, а сама она имеет много общего с моделью обычного коллекторного двигателя постоянного тока. Это открывает возможность построения различных наблюдателей, необходимых для реализации эффективных законов управления в следящих системах с бесконтактным приводом. Правда, такая модель содержит несколько фиктивных (абстрактных) переменных, что в отдельных случаях может вносить некоторые особенности в структуру синтезируемых наблюдателей.

В дальнейшем нами будет использоваться именно второй тип математической модели БМП. Основой для ее построения служат известные уравнения бесконтактного двигателя [1, 87]. При этом оставляем в силе и соответствующие допущения. В частности, магнитная цепь машины считается ненасыщенной, магнитный поток постоянных магнитов - постоянным, поле статора - круговым, реакция якоря и остаточный электромагнитный момент не учитываются. В отличие от указанных работ математическая модель БМП представляется здесь в структурной форме; кроме того, в ней выполнен учет запаздывания, вносимого УПУ.

Мгновенные значения напряжения, подаваемого на обмотку возбуждения ДПР, и напряжений, снимаемых с его вторичных обмоток, определяются выражениями % = «у sin Qh, «д.с = = kuy sin а, «д.к = дЫуСоз а, где «у - напряжение, которым управляется двигатель; Qh - несущая частота; - коэффициент трансформации ДПР; а = рп Ф - электрический угол, ф - механический угол поворота ДПР или СМ, отсчитываемый от од-

ной из неподвижных осей, связанных со статором машины; рп - число пар полюсов СМ и ДПР.

Считая, что УПУ, инерционность которого обусловлена в ос-новно.м наличием фильтров в ФЧВ, можно приближенно описать по каждому каналу динамически.м звеном первого порядка с постоянной времени Ту и коэффициентом передачи ky, получим следующие уравнения для фазных напряжений СМ:

ТуЫс-"«с =«ySina; (8.1)

7у«к + «к == kuy cos а, (8.2)

в которых принято k = kfily.

Для суммарных проекций фазных напряжений на продольную d и поперечную q оси ротора справедливо:

Ud = "Ksina -Uccosa; (8.3)

= «к cos а + «с sin а. (8.4)

Чтобы получить дифференциальные уравнения относительно переменных Ud и ы,, продифференцируем выражения (8.3) и (8.4) с учетом соотношений а = Q = р„и), где Й и со = ф - соответственно электрическая и механическая угловые скорости ротора. Тогда получим

«d = "Ksina-«cCosa + Q«; (8.5)

= ЫкС05а4-«csin а - Qud. (8.6)

Далее просуммируем уравнения (8.1) и (8.2), предварительно ум1южив их соответственно на sin а и cos а:

Ту (ucsin а-г «к cos а) + ы,, -= kuy. (8.7)

Наоборот, вычитая уравнение (8.2), умноженное на cos а, из уравнения (8.1), умноженного на sin а, получаем

Ту (ыс cos а - Ык sin а) - = 0. (8.8)

Тогда из (8.5) - (8.8) окончательно следуют искомые дифференциальные уравнения:

TyUa + Ud-QTyU,; (8.9)

TyU-{-u = kuy-~QTyUd. (8.10)

Отсюда также следует, что при Ту = О справедливы соотношения Ud = О, = kuy.