в) - -

Рис. 1.7. Нормирование передачи и сумматора: а - исходные элементы (в абсолютных единицах); б - нормирование в общем случае; в - нормирование с единичными коэффициентами

В соответствии с выражением (1.14) переход к системе относительных единиц основан на замене всех переменных системы произведениями их относительных значений на соответствующие базовые значения, что для звена, описываемого уравнением ifi = = kiXi (рис. 1.7, а), означает

yiyi б = kiXiXi б,

где «/,-, Xi - выходная и входная переменные в относительных единицах. Разделив последнее уравнение на уравнение того же звена в относительных единицах (рис. 1.7, б), т. е. на yi = kiXi, получим

ki-=kiXi6y~6, (1.15)

где ki - безразмерный коэффициент передачи звена.

Формула (1.15) представляет собой, по существу, уравнение, связи между коэффициентами передачи и базовыми величинами при переходе к безразмерной форме.

Для сумматора (рис. 1.7, а) можем записать

yy6 = XiXi6 + X2X26,

откуда

y = kiXi + k2X2,

где безразмерные коэффициенты согласования базовых значений определяются выражениями [см. (1.15)1

к1==-Х1б1уб; к2-Х2б1уб-

Структурные схемы, соответствующие звену с передачей и сумматору после нормирования, изображены на рис. 1.7, б. Приведенные нормированные схемы получаются максимально простыми, обеспечить приведение коэффициентов передачи к единице и устранить коэффициенты согласования при переходе к нормированной схеме, т. е. обеспечить выполнение условий (рис. 1.7, в)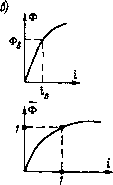

Рис. 1.8. Нелинейная электромагнитная цепь: а - электрическая схема; б.- структурная схема в относительных единицах; в - нормирование нелинейной статической характеристики

ki = 1 И = = 1. Это можно сделать, выбрав базовые значения переменных следующим образом:

Для пояснения сказанного рассмотрим пример нормирования системы уравнений (см. выше), описывающих динамический режим нелинейной электромагнитной цепи (рис. 1.8, а).

Запишем уравнения в размерной форме:

uir+WdOldt; if-O).

В качестве базовых значений переменных целесообразно выбрать их значения в установившемся режиме:

Фб = Фуст; 1б = ГНФб); иб = 1бг. Представив первое уравнение в виде

uueiier+WO&rm/dt

и разделив обе его части на ив, получим

ц =Г+ТбФ/Л.

Постоянный коэффициент Тс = WOJue, имеющий размерность времени, будем называть базовой постоянной времени (7, 15, 23, 24]. Как видим, благодаря принятому соотношению между Нб и Ie, переменная i входит в правую часть уравнения с единичным коэффициентом. Другой особенностью нормированного уравнения является то, что вместо двух параметров W я г в него входит один

сй5общенный параметр Те. Что касается нелинейности / = (Ф), то для нее можно записать

откуда

./-1(ФФе)==Г (Ф).

Таким образом, характер нелинейности при нормировании сохраняется, изменяется только масштаб (рис. 1.8, б). Нормированная структурная схема нелинейной электромагнитной цепи приведена на рис. 1.8, б.

Рассмотренные выше примеры были довольно простыми. Если имеем сложную многоконтурную систему, то переход в уравнениях к относительным единицам становится неудобным.

Это связано с тем, что в такой системе многие переменные являются общими одновременно для нескольких звеньев и поэтому не совсем ясно, какие из коэффициентов нормированной схемы можно привести к единице или другому требуемому значению, а 1(акие - нет. Вследствие этого определение правильной последовательности задания базовых значений переменных может оказаться затруднительным. Наиболее удобно нормирование математического описания системы осуществлять по структурной схеме. Это позволяет применить методику так называемого направленного нормирования структурных схем, разработанную Ю. А. Борцовым в конце 60-х годов, как такой переход к нормированной структуре (непосредственно по структурной схеме в абсолютных единицах), при котором заранее планируется приведение максимально возможного числа коэффициентов при линейных и нелинейных операторах к предписанным (желаемым) значениям, в частности, к единице.

Сущность методики направленного нормирования состоит в сле-дукмцем. Нормирование структурной схемы начинают с задания базового значения какой-либо переменной, обычно выходной. Хотя в качестве базового значения в принципе можно взять любое число, удобнее всего принять в качестве него номинальное значение переменной или ее значение в наиболее характерном установившемся режиме. Дальнейший выбор базовых значений переменных осуществляется непосредственно по структурной схеме и состоит в последовательном определении базовых значений входных и выходных переменных всех звеньев с учетом сформулированных исследователем требований к значениям их коэффициентов передачи в нормированной структурной схеме. В связи с этим все звенья структурной схемы могут быть условно разделены на две категории: свободно нормируемые и зависимо нормируемые. Свободно нормируемые звенья - это те звенья системы, коэффициенты передачи которых в относительных единицах назначаются путем соответст-вукмцего выбора базовых значений входных и выходных перемен-