Рис. 1.1. Структура оптимизируемого контура

Если выбрать

2Гр (Гр+1)

(1.1)

(1.2)

Передаточная функция замкнутого контура по управляющему воздействию в соответствии с выражением Wa (р) = W (р) [ 1 + + Wip) ]-1 будет

(р)=-

(1.3)

rV + 21Тр + 1

где Т = J2 Т; 1=1/ 0,707.

Логарифмические частотные характеристики (ЛЧХ), соответствующие передаточной функции W (р), изображены сплошными линиями на рис. 1.2. При ступенчатом управляющем воздействии выходная величина в первый раз достигает установившегося значения через время 4,7 Т; перерегулирование составляет 4,3 % (рис. 1.3, а). Длительность переходного процесса не зависит от постоянной времени объекта То и определяется только малой постоянной времени Гр,. Такой способ настройки называется настройкой на оптимум по модулю (ОМ). Наиболее простое объяснение этого термина состоит в том, что при настройке на ОМ стремятся в широкой полосе частот сделать модуль частотной характеристики замкнутого контура близким к единице [98].

Реализация настройки на ОМ возможна и при других передаточных функциях объекта.

Если Wo (р) = koKXop), то должен быть использован пропорциональный регулятор с передаточным коэффициентом

k = To!{2TJiok,).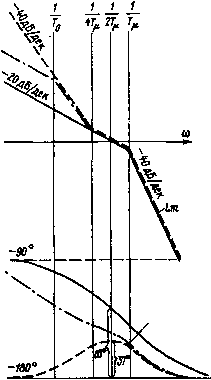

Фаза WQiS)

Рис. 1.2. Логарифмические частотные характеристики разомкнутого контура при стандартных настройках: на ОМ (сплошные кривые); на СО (штриховые); при W (р) - kJ(Tp + 1) и ПИ-регуляторе (штрихпунктирные)

О) 1

%в 0

15 го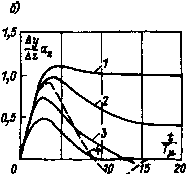

Рис. 1.3. Переходные процессы в контуре при стандартных настройках и скачке: а - управляющего воздействия; б - возмущающего воздействия, "тройка: на СО - штриховые кривые; иа ОМ - сплошные кривые при oiTfi, равном оо (кривая /); 20 (кривая 2); 4 (кривая 3); 2 (кривая 4)

При отсутствии в контуре большой постоянной времени и Wo{p) = kfi, регулятор должен быть интегрирующим:

Mp) = h/p (1-4)

при Рр = 1/(2ГроМ-

Если объект содержит две значительные постоянные времени То и То1, т. е.

Цо(р)- ,„, „ , „ (1.5)

ТО аналогичный результат может быть получен, если применить пропорционально-интегрально-дифференциальный (ПИД) регулятор с передаточной функцией

выбрав Рр в соответствии с формулой (1.1) и приняв Хр = Го,

Тр2 ~ 7*01.

Для объекта в виде апериодического звена запишем передаточную функцию замкнутого контура по возмущению:

А</(р) Мо 1

Аг{р) Т„р+1 l + W(p)

где Ау (р) - выходная переменная.

Подставив сюда W {р) из выражения (1.2) для передаточной функции контура, настроенного на ОМ, и умножив обе части равенства на a = Tol{2TJiJio), получим

Дг(р) Гр„+1 2Гр,р (Гр,р + 1) + 1

При такой записи становится очевидным, что длительность и вид переходного процесса по возмущению определяются соотношением постоянных времени То и Гр, (рис. 1.3, б). При Го->оо переходный процесс приближается к процессу в настроенной на ОМ системе с объектом в виде интегрирующего звена и пропорциональным регулятором. Тогда выходная величина с незначительным перерегулированием стремится к статической ошибке

уст Oz То

Уменьшение статической ошибки (а при бесконечно большом коэффициенте усиления регулятора в статическом режиме сведение ее к нулю) в контуре с объектом в виде интегрирующего звена может быть достигнуто путем использования ПИ-регулятора. Если выбрать Рр в соответствии с формулой (1.1), но принять Тр = 47",