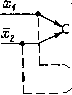
<1

Рис. 1.16. Определение базовой постоянной времени интегрирующего звена

интегральным методом

нуля ДО установившегося (базового) значения. Учитывая, что для такого процесса Ал:вых = Аловых, б = 1, а Хвх = u-i, применяя для определения Тб уравнение (1.22), получим

Гб = Ий-0.

в этом случае для определения базовой постоянной необходимо произвести интегрирование площади, заключенной между кривыми относительных переменных входного напряжения и тока, изменяющихся по произвольному закону.

Постоянная времени якорной цепи двигателя Гя может быть определена из физического процесса нарастания тока якоря до любого установившегося значения при подаче на якорную цепь соответствующего пониженного напряжения и заторможенном якоре двигателя. Для такого процесса можно записать в нормированном виде

Интегрировать Хех, изменяющееся по произвольному закону, можно с помощью дополнительного (измерительного) интегратора с известной постоянной времени Ги- Схема для определения постоянной времени интегрирующего звена ДСС показана на рис. 1.16. По окончании процесса интегрирования за период -выходная величина звена ДСС - объекта измерения изменится на величину

Aw-SBxd/. (1.23)

Подавая одновременно ту же входную величину на измерительный интегратор, по окончании процесса измерения получим

x„==-:r~lxъxdi.

1578

сравнивая эти выражения, находим

с помощью интегрального метода можно решить и другую задачу - при известной (в частности, экспериментально определенной) постоянной времени интегрирующего звена определять текущие (установившиеся) значения выхода этого звена путем интегрирования изменения входной величины произвольным образом на любое, задаваемое исследователем, известное значение. Методика такого эксперимента основана на формуле (1.23) и может оказаться полезной, например, при снятии статических характеристик Ах1ых = / (-"в") звеньев, выходная величина в статике у которых определяется с трудом. К числу таких звеньев относятся, например, цепи возбуждения крупных двигателей, когда в качестве выходной величины рассматривается поток возбуждения. Величина Г„ может быть произвольной, хотя для удобства отсчетов при измерениях ее целесообразно принимать равной 1 с. Еще раз отметим, что в тех случаях, когда входная величина испытуемого звена не может быть получена в явном виде, ее приходится формировать из реальных физически воспроизводимых входных сигналов путем алгебраического суммирования на входе измерительного интегратора (на рис. 1.16 показано пунктиром). Столь простая реализация интегрального метода применима к широкому классу электромеханических систем, элементы которых могут быть описаны системой дифференциальных уравнений первого порядка вида

at k=l q=l

где (x) - функциональные зависимости от координат системы, в том числе выходной координаты t-ro звена; и,, (t) - внешнее воздействие на входе t-ro звена.

1.4. Векторно-матричные модели и их преобразования

Уравнения состояния и детализированная структура многомерного объекта. Главной особенностью «современной теории управления» [2, 31, 79] является рассмотрение систем преимущественно во временной области на основе понятия пространства состояний. При этом рассматриваются в общем случае многомерные системы, т- е. системы произвольного порядка с многими входами и выходами, в связи с чем широко используются язык векторно-матричных уравнений и аппарат линейной алгебры. Фундаментальным понятием современной теории управления является понятие состоя-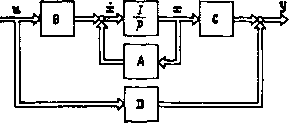

Рис. 1.17. Математические модели многомерного объекта в пространстве состояний: а - структурная схема, соответствующая уравнениям состояния; б - векторио-матричиая структурная схема; в - то же для линейной системы

НИЯ. Говоря коротко, состояние системы в момент времени есть такая совокупность сведений о ней, наличия которой вместе с некоторым возможным входным воздействием, заданным на интервале времени t ti, достаточно для однозначного прогнозирования поведения системы в каждой точке этого интервала [2, 311.