производится их аналоговая фильтрация и масштабирование перед подачей на вход аналого-цифрового преобразователя ЭВМ управ-лякнцего комплекса. В ЭВМ формируются массивы данных, вычисляются амплитуды и фазы при данной частоте, результаты расчетов выводятся на печать. На управляющий комплекс возложены также функции контроля и управления. В случае превышения напряжением ГНЧ или током якоря предельно допустимых значений выдается сигнал оператору, а ГНЧ отключается от входа АСУ ЭП, что предотвращает возникновение аварийных режимов. При изменении частоты от 0,1 до 10 Гц (от 0,628 до 62,8 рад/с) по каждому из каналов снимается от 50 до 100 точек за период колебаний. Для получения достоверной оценки в расчет могут быть введены данные по нескольким периодам. После завершения формирования массивов сцгнал ГНЧ отключается от входа системы.

В основу вычисления ЛЧХ положен алгоритм дискретной фильтрации Фурье [64]. Определение вещественной и мнимой частей частотной передаточной функции при возбуждении объекта синусоидальным входным сигналом и (/) = Uosin a>t может быть выполнено в дискретной форме в соответствии с выражениями:

t"=0

*=iZ*<"("-r)

где при данной частоте N == 2я/ (соГо) - определенное с учетом периода дискретизации число отсчетов за период; у (tt) - выходная величина в i-й момент отсчета; i - номер момента отсчета. Таким образом, процедура определения вещественной и мнимой частей частотной передаточной функции сводится к умножению выходного сигнала в дискретные моменты времени на sin {2ni/N) или cos {2ni/N) и вычислению в определенном масштабе суммы этих произведений за период.

С целью повышения точности определения ЛЧХ измерение производится в течение нескольких периодов с усреднением результата по рекуррентным формулам:

где Uk и Vk определены иа к-м периоде, а волной сверху отмечены средние значения.

Необходимая длина выборки определяется в процессе измерения в зависимости от среднего квадратического отклонения средних значений характеристик, которое не должно превышать неко-

торого заданного малого значения е. С этой целью вещественная и мнимая частотные характеристики рассматриваются как случайные величины с гауссовским распределением, для которых оценки дисперсий определяются как

От, -=

k(k-l) 1

k{k-l) *т

(4.3)

Процесс измерений заканчивается, когда выполняются условия

л/и < е; /Dy <е.

Структурная схема алгоритма определения частотных характеристик приведена на рис. 4.3.

Вычислительный процесс определения частотных характеристик разделен на два раздела, выполненных с приоритетами разного уровня. В оперативном разделе вычисляется задающий сигнал, опращиваются датчики й выполняется алгоритм управления. В фоновом разделе выполняется алгоритм определения частотных характеристик.

По определенным на объекте экспериментальным логарифмическим частотным характеристикам принимается конфигурация модели и находятся частоты резонансов и провалов аппроксимирующих логарифмических амплитудных частотных характеристик, т. е. постоянные времени, входящие в передаточные функции преобразованной структурной схемы (см. табл. 4.1). В случае кольцевой схемы, где частоты резонансов есть T~•, Г"; Г, а частоты провалов - Гг написать:

Г4; Гб; Г/, на основании данных табл. 4.1 можно

Acoi (р)

F(P)

Аш,{р) ту + 1

А 0)1 (р)

АЮ4 (р) Ащ (р)

F(P)

Пр-т

F(P)

(4.4)

где F{p) = TlTlTlp + {T\Tl + Tl) + 1.

+ ГзГ + TlTb p + {T\ + Tl +

Начало

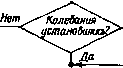Рормирование массива данных за период

Определение

Определение DgfinoipofmifJxif.S)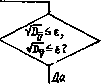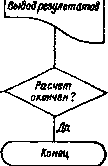

Рис. 4.3. Алгоритм определения ЛЧХ

Приравнивая коэффициенты полиномов числителей и знаменателя соответствующим коэффициентам в передаточных функциях (4.1), можно получить систему из семи нелинейных алгебраических