нове его модели, имеет нулевой корень, что исключает возможность ее настройки при отключенных связях наблюдателя и регулятора.

Рассмотренные в настоящем параграфе наблюдатели относятся к наблюдателям полного порядка, восстанавливающим и те координаты системы, которые могут быть измерены непосредственно. Существует возможность построения редуцированных наблюдателей, восстанавливающих лишь неизмеряемые координаты [58]. Однако к достоинствам описанных наблюдателей полного порядка можно отнести то, что в основе их лежит модель, структурно повторяющая объект, что упрощает их проектирование, наладку и контроль в процессе функционирования.

ГЛАВА ТРЕТЬЯ

МИКРОПРОЦЕССОРНАЯ РЕАЛИЗАЦИЯ СИСТЕМ УПРАВЛЕНИЯ ЭЛЕКТРОПРИВОДОМ

3.1. проектирование цифровой системы управления электроприводом по аналоговому прототипу

При цифровой реализации АСУ ЭП связь между непрерывным объектом и ЭВМ в контуре регулирования, являющейся дискретным устройством, осуществляется через преобразователи аналоговых величин в цифровой код (АЦП) и цифрового кода в аналоговую величину (ЦАП). Функциональная схема одноконтурной системы в предположении, что сигналы квантуются синхронно с периодом дискретизации То, приведена на рис. 3.1, а.

Входной сигнал иу и сигнал, пропорциональный истинному значению регулируемой величины д;* в цифровой форме, обрабатываются с помощью ЭВМ, выполняющей роль регулятора. Цифровой сигнал на ее выходе и* преобразуется ЦАП, благодаря чему,аналоговый сигнал и на входе непрерывного объекта остается постоянным в течение периода дискретизации.

Сигналы АЦП и ЦАП квантованы по уровню, вследствие чего системы управления непрерывными объектами с ЭВМ в контуре регулирования относятся в общем случае к классу дискретных нелинейных систем. Однако, если разрядность преобразователей достаточно велика, в первом приближении можно пренебречь квантованием сигналов по уровню, заменив нелинейные статические характеристики АЦП и ЦАП линейными и введя коэффициенты передачи

где Ai - приращение аналоговой величины х на входе АЦП, соответствующее изменению выходной величины х* на одну дискрет-

Непрерывный объект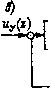

Рис. 3.1. Схема цифровой одноконтурной системы: а - функциональная;

б - структурная

нуюединицу; Aj-• приращение выходного напряжения ЦАП и при изменении на одну дискретную единицу входного сигнала и*. Тогда математическое описание АСУ ЭП с ЭВМ в контуре регулирования может быть представлено линеаризованной структурной схемой на рис. 3.1, б, на которой обозначено: Wp (z) - передаточная функция цифрового регулятора при описании алгоритма его работы в области комплексной переменной г; Wso ip) = - (1-е~)/р - передаточная функция экстраполятора нулевого порядка, Woip) - передаточная функция объекта управления. В схему введено звено чистого запаздывания е~»«, учитывающее, что на вычисление управляющего воздействия в соответствии с передаточной функцией регулятора Wp(2) ЭВМ затрачивает время Тм.

Таким образом в АСУ ЭП объект управления описывается системой дифференциальных уравнений или передаточными функциями в области комплексного аргумента р, а алгоритм работы ЭВМ -• разностными уравнениями или передаточными функциями в области аргумента z дискретного преобразования Лапласа.

Могут быть рассмотрены два подхода к проектированию цифровой системы управления электроприводом.

Первый подход основан на синтезе системы, рассматриваемой как непрерывная и описываемой в области комплексной переменной величины р. Требуемый алгоритм работы цифровой системы управления электроприводом определяется при этом в результате дискретной аппроксимации аналогового прототипа.

При втором подходе дискретной аппроксимацией заменяется описание непрерывного объекта, в результате чего вся система оказывается описанной в области комплексной переменной г, а алго-

ритм работы цифровой части определяется в результате синтеза дискретной системы.

Основу проектирования цифровой АСУ ЭП при первом подходе составляет математическое описание аналоговой системы, структура и параметры регулирующей части которой уже определены, например, теми методами, которые описаны в гл. 2. При этом должны быть записаны передаточные функции, связывающие управляющий сигнал, действующий на входе непрерывного объекта, с внешним входным воздействием и координатами системы, по которым осуществляется ее замыкание.

Для представленной в наиболее общем виде системы на рис. 2.21 математическое описание задается системой трех уравнений:

и =fep. сА«у- А«о. с; А«о. с = к (DiXi + DiiXii);

Xii = A„Xn -LCaXii-f Lyii-f ВнУь

на основании которых выражение для управляющего сигнала

« = fep. сА«у + к !fD,-f 0,1 (pi -Ан-f LC„)-B„C,]xi-f + D„(pl-A„-f LC„)- LC„x„).

Если обратиться к системе (рис. 2.23), описание которой дано на стр. 110, то после подстановки сюда соответствующих матриц и последующих преобразований это выражение может быть записано в виде

u=kp,,Miy-W, (р) дгз - (р) х„

где Wi (р) и W2 (р) - передаточные функции, характеристики которых при цифровой реализации АСУ ЭП должны быть аппроксимированы соответствующими функциями Ui (2) и (2).

Аппроксимация передаточной функции может быть выполнена с использованием таблицы 2-преобразования. В этом случае передаточную функцию высокого порядка предварительно раскладывают в сумму дробно-рациональных членов, каждому из которых можно найти соответствие в таблицах изображения решетчатых функций [101.

Другим широко используемым методом перехода от непрерывного математического описания к дискретному является подстановочный, основанный на дискретной аппроксимации интеграторов и подстановке вместо комплексной переменной одного из выражений

8 Заказ № 398 ИЗ