ных этих звеньев. Для i-ro звена с коэффициентом передачи ki назначение требуемого безразмерного коэффициента передачи ki выполняется путем определения базового значения входной переменной xiQ ПО базовому значению выходной ;б или, наоборот, определения б по х,б в соответствии с выражениями, получаемыми из формулы (1.15);

Xi6 = kikTy;e или i/ic ==kTkiXic. (1-16)

Эги выражения имеют общий характер и отвечают всем случаям нормирования структурных схем. В частном случае, если необходимо сохранить нормированный коэффициент по значению равным исходному коэффициенту, т. е. ki = ki, необходимо выбрать Xi6 = г/гб. Если же нормирование звена необходимо выполнить с приведением его коэффициента передачи к единице, т. е. /г = 1, выбирают Xi6 = kjyiu- Для нелинейных статических характеристик вида у f {х} «единичное» нормирование (/(1) = 1) обеспечивается выбором Хб = /" (г/б) или ув ~ f (хб)- Аналогично для блока умножения z = ху при выборе ze == хсуб получаем z - ху. Как указывалось ранее, нормирование сумматоров во избежание появления на безразмерной структурной схеме дополнительных согласующих коэффициентов целесообразно осуществлять таким образом, чтобы базовые значения всех переменных, относящихся к сумматору (задающих сигналов обратных связей, выходных), были равны друг другу:

Ххб - Хф- - Аю. с. б = 20, с. б ~ . • - Х-б- (117)

В результате применения описанной процедуры свободного нормирования для некоторых звеньев структурной схемы базовые значения как входной, так и выходной переменной окажутся уже ранее выбранными и, следовательно, заданными принудительно. Такие звенья будем называть зависимо нормированными. Для них переход к относительным единицам производится путем определения значения зависимого коэффициента передачи согласно (1.15) по формуле

kiki-.

Число таких зависимо нормируемых коэффициентов структурной схемы, т. е. коэффициентов, значения которых не могут быть выбраны произвольно, определяется выражением

Пз~=1 - пг + г,

где / - общее число пapaллevьныx ветвей во всех согласно-параллельных соединениях структурной схемы; т - число независимых параллельных соединений; z - число замкнутых контуров структурной схемы. Если п - полное число коэффициентов схемы,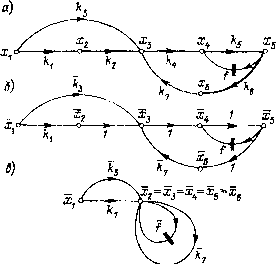

Рис. 1.9. К определению числа свободно нормируемых звеньев структурной

схемы (графа)

ТО ЧИСЛО свободно нормируемых коэффициентов может быть найдено как

Из теории графов известно, что число свободно нормируемых звеньев структурной схемы (графа) определяется его деревом. Это положение может быть использовано при нормировании для проверки. Дерево представляет собой связный подграф данного графа, включающий в себя все его узлы (т. е. переменные системы), но не имеющие ни параллельных ветвей, ни контуров.

Для пояснения сказанного рассмотри.м изображенный на рис. 1.9, а граф нелинейной автоматической системы. Он содержит восемь ветвей, в том числе одно параллельное соединение (т = 1), состоящее из двух ветвей (/ = 2), а также два независимых контура (г = 2). Следовательно,

«,--2-1-4-2=3,

откуда

Псв - 8-3 - 5.

Таким образом, пять коэффициентов могут быть пронормированы по нашему усмотрению. Например, пусть задана следующая программа свободного нормирования:

На рис. 1.9, а жирными линиями показано одно из возможных деревьев, а именно то, которое соответствует программе нормирования. Все остальные ветви {k, й,, /) образуют так называемые дополнения графа и соответствуют зависимым коэффициентам. Из рисунка хорошо видно, что появление зависимых коэффициентов связано с наличием в графе параллельных ветвей или замкнутых контуров.

Порядок определения базовых значений переменных при нормировании по заданной нами программе может быть, например, следующим. Выбираем Хьб = Хъусг- Далее в соответствии с вариантами (1.16) находим

х(, = 856; Хцб = Й5 л:5б; лгдб = 4 хе,;

Хб = 2 Хб, Xi6 = Х26

Получившийся в результате нормирования граф в относительных единицах и эквивалентный ему граф показаны на рис. 1.9, б и рис. 1.9, в. Зависимые коэффициенты определим по формуле (1.15):

Нелинейная функция / - также зависимо нормируемая:

Ч = -- f (хьхб) = / fe).

Для проверки правильности расчета коэффициентов нормированной структурной схемы имеются еще два общих правила, вытекающих из правил линейной алгебры:

1. Коэффициент передачи любого прямого пути (направленной последовательности звеньев) в нормированной структурной схеме knp должен быть равен соответствующему коэффициенту структурной схемы в абсолютных единицах knp, умноженному на отношение базовых значений входной и выходной переменных этого пути:

fenp=Anp „ • (1-18)

•вых.б

2. Коэффициент передачи любого контура после перехода к безразмерной структурной схеме сохраняет свое значение:

(1.19)

Применим второе правило, например, к контуру, образованному переменными х, х, Хь и Xf. Для исходного графа k = = kk-Jiki. Для нормированного графа

1и = k, - k, = k, = k,k,kA = k„

"Зб 4 -46

ЧТО подтверждает правильность нормирования. 26