восстанавливается (оценивается) с помощью наблюдателя. В отличие от наблюдателя, описываемого уравнением (1.41) и имеющего тот же порядок, что и объект, здесь применен так называемый наблюдатель пониженного порядка. Он оценивает только ту координату, которая непосредственно не измеряется. Уравнения наблюдателя имеют вид

2 = - (Оа + ка) ~ axi + flju;

X2==Z+ ХХу-.

с учетом первого уравнения объекта х = ах найдем

2 =z + Xxi= -ах-кахх-х-ах + аи.

Вычитая из этого уравнения второе уравнение объекта х = = - ajAi-ах + йф, после простейших преобразований получаем

г - Xi = - {аг + ка) {х-х), откуда следует, что

X, (О = Х2 it) + R {0)~х, (0) J е- <"+

Как видно из последнего выражения, при/->св х-х, причем необходимая скорость сходимости х кх может быть задана выбором значения параметра Х.

ГЛАВА ВТОРАЯ

АНАЛИЗ и СИНТЕЗ СИСТЕМ УПРАВЛЕНИЯ СКОРОСТЬЮ ДВУХМАССОВОГО УПРУГОГО МЕХАНИЗМА

2.1. Математическое описание двухмассовой электромеханической системы с упругостью первого и второго рода

При рассмотрении автоматизированных систем управления электроприводом часто предполагается, что кинематическая связь между двигателем и исполнительным органом (ИО) не подвержена упругим деформациям. Если при этом связь не содержит зазора, то ско-

рость двигателя и приведенная к двигателю скорость механизма равны между собой не только в установившемся режиме, по н в переходных- процессах, а момент инерции привода является суммой моментов инерции двигателя, редуктора и приведенного к двигателю момента инерции исполнительного органа. Изменение момента •нагрузки на механизме в этом случае эквивалентно изменению момента нагрузки на двигателе. Во многих случаях идеализация, основанная на представлении о жесткой связи двигателя и исполнительного органа, оказывается допустимой. Это определяется тем, что частота собственных упругих колебаний механизма оказывается значительно выше частоты, определяющей быстродействие автоматизированной системы управления электроприводом. Если это условие не выполняется, то пренебрежение упругостью при анализе и синтезе системы может привести к ошибочным результатам. Чем,выше быстродействие системы управления, тем больше вероятность того, что влияние упругости на работу системы управления электроприводом будет заметным.

Рассмотрению динамики системы управления электроприводом реального механизма предшествует создание модели механизма. Эта модель, с одной стороны, должна быть достаточно подробной для того, чтобы соответствующее ей математическое описание было достоверно в области существенных частот, с другой стороны, она должна быть по возможности простой, чтобы изучение динамических процессов на ее основе было реально осуществимым. Критерием допустимости принятого упрощения является удовлетворительное совпадение результатов теоретических расчетов с результатами эксперимента.

Реальный механизм, строго говоря, почти всегда представляет собой систему с распределенными параметрами. Однако в большинстве случаев вполне удовлетворительный результат может быть получен при представлении механизма в виде системы с сосредоточенными параметрами. При этом общепринятыми являются следующие допущения [52]:

а) силы и моменты, действующие в системе, приложены к сосредоточенным массам, которые не деформируются;

б) упругие звенья невесомы и характеризуются постоянной жесткостью, т. е. постоянным коэффициентом пропорциональности между мо.ментом (силой) и деформацией;

в) волновым характеро.м распространения де(})ормацни можно пренебречь.

Наиболее простым является широко распространенный случай, когда якорь двигателя, питающегося от регулируемого источника, например тиристорного преобразователя, и исполнительный орган, связанный упруговязкой передачей, образуют двухмассовую электромеханическую систему (рис. 2.1, а). При этом под моментом инерции первой массы понимается момент инерции двигателя и.редуктора, а под моментом инерции Jo - не приведенный к дви-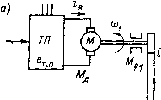

г 2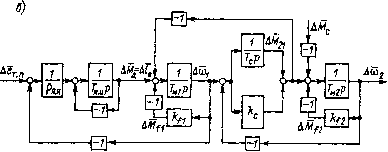

Рис. 2.1. Двухмассовая электромеханическая система с упругостью первого рода: а - функциональная схема: б - линеаризованная нормированная детализированная структурная схема

гателю момент инерции ИО. Считается, что упругость сосредоточена в длинном вале и муфтах, соединяющих редуктор с ИО.

Предположи.м, что под действием электромагнитного .мо-.мента УИд, приложенного к ротору, и мо.мента Мс, приложенного к ИО, упругая передача скручена на некоторый начальный угол. После исчезновения внешних моментов в системе возникнут затухающие колебания. Если двигатель отключен от источника питания, затухание колебаний будет происходить только под действием сил трения, на преодоление которых необратимо расходуется энергия, запасенная в упругой системе. Для описания этих сил обычно используют упрощенные представления. Оставаясь в рамках линейной теории, .можно предполагать, что колебания затухают из-за сил внутреннего трения в упругом звене, пропорциональных разности скоростей первой и второй масс col и coi, а также из-за внешнего вязкого трения на первой и второй массах, которые в первом приближении могут быть приняты пропорциональными скоростям соответствующих масс.