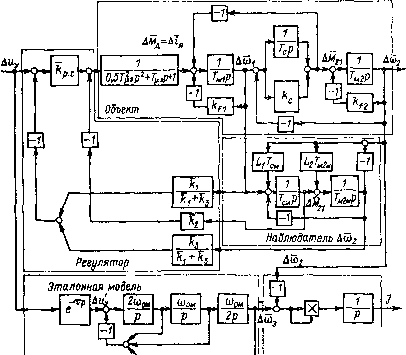Вычисление рункиионала

Рис. 4.8. Структурная схема АСУ ЭП с автоматизацией настройки

Обычно достаточно в качестве эталонной модели использовать модель третьего порядка с передаточной функцией

Асоз (р)

Д«у (Р)

iWomP

Если АСУ ЭП, имеющая более высокий порядок, рассчитывается исходя из стремления получить переходную функцию по выходной Координате, соответствующую стандартной форме Баттерворта, то и эталонную модель целесообразно настраивать по Баттерворту, приняв 01 = 02 = 2. Значение среднегеометрического корня характеристического полинома модели Юо„ надо в этом случае выбрать так, чтобы расчетные переходные характеристики АСУ ЭП и модели наилучшим образом совпадали. Звено чистого запаздывания е-Р на входе модели введено для обеспечения лучшего совпадения начальных частей переходных характеристик. На рис. 4.9,

Q,SO

0,ZS

Рис. 4.9. К определению параметров звена чистого запаздывания эталонной модели

где приведены характеристики, соответствующие стандартным формам Баттерворта второго-восьмого порядков, показано, как надо выбрать т, если настройка АСУ ЭП производится исхо;я из стремления получить характеристику Баттерворта пятого порядка, а модель имеет третий порядок. Длительность расчетного переходного процесса определяет значение Т в функционале (4.12).

В схеме на рис. 4.8 в процессе настройки могут варьироваться коэффициенты регулятора ki, и к; коэффициенты наблюдателя /х и /2, а в более общем случае - и постоянные времени наблюдателя Т<м и Гмгм- Ниже варьируемые параметры обозначены через а/., где /= 1, 2 ... п.

Для минимизации функционала (4.12) могут быть использованы различные методы нелинейного программирования. Одним из наиболее эффективных и легко осуществляемых на ЭВМ является метод поиска по деформированному многограннику (метод Нелдера и Мида) [86]. Соответствующая структурная схема алгоритма представлена на рис. 4.10.

В качестве исходных данных вводятся: число варьируемых параметров /г, начальные значения варьируемых параметров анач и шаги их изменения Аа. Матрица планирования А (i, /) вычисляется на оснований нормированной матрицы на симплексе размером (д + 1) X п:

M(t, /) =

1

где mi = (Vrt+l -l)/(rtV2); ma - (V«+1 -V")-160

Рис. 4.10. Алгоритм процесса автоматической настройки

Элементы матрицы А (i, /) определяются в соответствии с выражением

где i - номер вершины многогранника (номер строки матрицы А (i, /); j = U 2 . . . п - номер варьируемого параметра; mtj- элемент t-й строки и /-го столбца матрицы М (i, /).

В каждой вершине многогранника, обозначаемой как

ailanaaais . . . щ], вычисляется функционал J (ар) при t = l, 2 . . . (n+l) н k - 0. Индекс «» соответствует номеру шага в направлении минимизации функционала.

Из полученных значений выделяются наихудшее (максимальное) J (ак*) и наилучшее (минимальное) J (а**) значения функционала в вершинах Ли/.

Вычисляются координаты центра тяжести многогранника

/=1, 2 . . . п и отраженной вершины

т-П-

15,21

Начало

Ввод исходных данных

r-S-

Вычисление матрицы планирования A(i,j)

Вычисление „ (рункционала 3{a,i) д вершинах ииово-грЛка (£=iJZ...n+J)

. д

Выделение

шшмалыюго (ян)

а миншшаногв ) аначений днрвщцоиш

rz-6

Вычисление коорЛат центра тяжести инвщтннит к;

ишчвния 3(лп+2)

Вычисление jmauHom отражештОшиы

гдеа>1. В отраженной вершине вычисляется функционал J (п+з). Если выполняется условие

У(а<*Л)<У(аП, (4.13)

то производится операция растяжения, в результате которой опре-