может быть введен интеграл путем замыкания еще одного контура через интегратор И (см. рис. 2.10, а). Передаточные функции по управлению в этом случае приобретают вид:

.1э ip*) = {y4pl+i)/Rip*),

(2.26)

где = р/щи R (р*) =

YT 1 (Р*У> == Ги - норми-

2(Й1 + йз)

рованная постоянная времени интегратора. Приравнивая нормированный характеристический полином

Нг(р,) = р1 + р1+(- + -)р1 +

-эФм

о 2 ""эумн

полиному

fi ip*) = (р!+dip!+р!+зр*+1) (р!+ьщр+(о!),

в котором di = ds = 2,6; = 3,4 (распределение Баттерворта 4-го порядка), а со = co/woi, можно аналогично изложенному выше получить выражения для коэффициентов регулятора в виде:

и 2,6т„ , .

1 =-ai(Ty; тэ);

2 = (3,4ту -1) а2 (Ту; тз);

Аз = 2,6т„тз (ту; Тр,э) - Ai; Ти = 2,6а4 (Ту; тэ),

(2.27)

где стремящиеся к единице при Tjj3->-0 сомножители определяются выражениями:

1 , .\ /. „ , I

ai(Ty; т1э)=---1-f 4

«2 (Ту; Тэ) = 1+Т,

тз (2,8ту-ЬЗ,4) 6,2&4 3,4т2-1

2,2

1 - 1,ЗТ

2.6 + Тцэ

-6,75

Построенная таким же образом, как в статической системе, зона допустимых соотношений параметров показана на рис. 2.13 штриховыми линиями. Из сравнения с соответствующей номограммой для статической системы (сплошные линии на рис. 2.13) видно, что если ограничение на быстродействие связано с предельно допустимым значением тэ (участок аб), то при одинаковых соотношениях Тцэ/Ту допустимое значение Ту примерно на 10 % ниже, чем в статической системе, что с учетом возрастания длительности процесса, соответствующего четвертому порядку по сравнению с процессом третьего порядка, дает увеличение длительности переходного процесса примерно на 30 % по сравнению со статической системой. Если же тэ мала и ограничение на быстродействие связано со стремлением ограничить бросок скорости двигателя, то из зависимости Ту.пред = / (у) для системы с астатизмом по возмущению (штриховая кривая на рис. 2.13) среднегеометрический корень о)о1 можно сделать больше, чем ©о ь статической системе.

Передаточные функции по возмущению имеют вид:

Д Мс (Р*)

ДМ1 (р*) /

pl + Apl + Bpl + Cp,+d

Hi (р.) fpl-Gp,+h Ml (р,)

Коэффициенты Л, 5, С и G имеют те же выражения, что и в формулах (2.25). Значения коэффициентов d, f и к приведены в табл. 2.2. При тэО переходный процесс в системе с обратными связями по ©i, М21 и (1)2 зависит только от значения-у/у Ту (рис. 2.16, а). При переходе от связи по М 21 к связи по производной от «2 реакция на возмущение оказывается зависящей от л/у Ту и от у. Если у « 1, то система приобретает астатизм 2-го порядка по возмущению, а нормированный переходный процесс Асо2/АМс = ™ f (*»м) остается одинаковым независимо от параметров объекта. Значение л/у Ту определяет характер изменения скорости двигателя (рис. 2.16,6). При коэффициентах соотношения масс у> 1 и характер изменения скорости двигателя и характер изменения скорости ИО будут различными при разных л/у Ту. В качестве примера кривые Аюг/ДМс = / (/©oi) при у = 10 и трех значениях Ту показаны на рис. 2.16, в. Если выбор параметров произведен в со-

- if%=1,8 08

1 \ \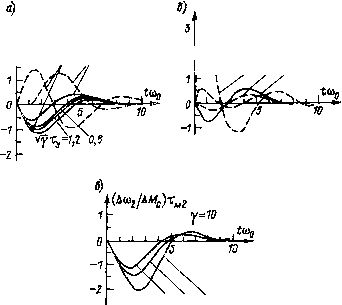

Рис. 2.16. Характер переходных процессов по всз.мущению в системе с введением интеграла при Тцэ -> 0: а - при замыкании по вектору состояния механизма; б, в - при переходе от связи по Магксвязи по раьгдля разных

значений у и Ту соответственно [----Тм. (Дш/ДМс);---

т„2(Д сОг/ДМс)!

ответствии с номограммой рис. 2.13, переходные процессы по длительности и значению динамического отклонения будут отличаться от приведенных на рис. 2.16 не более чем на 20 %.

2.4. Возможности настройки контура скорости системы подчиненного регулирования с упругостью без изменения ее структуры

Замыкание двухмассовой электромеханической системы по вектору состояния механизма - не единственный способ реализации АСУ ЭП с упругостью, в некоторых случаях удовлетворительный результат может быть достигнут более простыми средствами, в частности, в резу.тьтате правильного выбора коэффициента регулятора скорости kp.c (см. рис. 2.7). Будем предполагать пока, что малые постоянные времени в контуре скорости пренебрежимо малы: W/iip) » 1, Гт.г = О, а затем определим предельно допустимое значение Tэ, при котором могут быть реализованы настройки,