an = = cos (P Го); flia = 1

21 =

7-M2P

sin(pTo);

sin(pTo);

Tcf>

sin(PTo); bi2-l-cos(pro); p =

m2 Vv Ту

Матричная передаточная функция дискретно аппроксимированного объекта имеет вид

W(2) = {zl-A*)- В* =

F(z)

gn (2)

. g2i (г) J

F (z) = det (zl - A*) = 2cos (рГо) 2 + 1;

(г)-

Tcf>

sin (рГо); (z) = [1 - cos (рГо)] (z+ 1).

В результате решения уравнения

= HO{z),

lg2l (2)

в котором Я" (z) соответствует (3.6), можно определить коэффициенты регулятора:

[cos (pro)-cos (О.ТОУсооП) е-°»°"»-0,5 (l

2 = [cos (рГо) -cos (0,707шоГо) е

-О.ГОТшоГо

Х[1-С05(рГо)Г.

+ 0,5 с

-1,414ш„Г„

1)]х

Если за Я„ (2), как и при синтезе регулятора, принять стандартную форму (3.6), при соо = ©он, то значения коэффициентов наблюдателя будут:

/; = {2cos (рГо) [cos (рГо) -cos (0,707шо„Го) е-°°"о"о]- +

sin (рГо)

+ е-"н-о 1);

= 2 [cos (pro)-cos (0,707со„„Го) ].

Структурная схема разработанной таким образом цифровой системы управления непрерывным объектом показана на рис. 3.7. Из нее следует, что для реализации наблюдателя и регулятора в ЭВМ необходимо вычислять следующие разностные уравнения:

(п + 1) = anXi (п) + ai2X2 (п) + 11 [х2 (п)-х (п)] + coi (п);

Х2{П+1) = aliXi (П) + 0222 (") + 2 (rt) -2 («)] + 21©l (п); й(п+ l) = fe2«y (П+ 1) -feixi(n+ 1) -fe22{« + !)•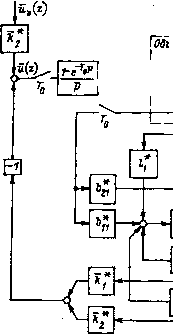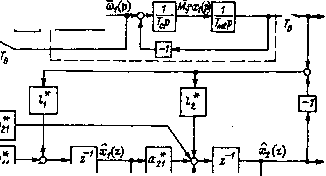

Рис. 3.7. Структурная схема цифровой системы управления непрерывным

объектом

Достоинства рассмотренного подхода к разработке дискретных систем управления непрерывными объектами определяются, в первую очередь, применением векторно-матричного описания, обеспечивающим высокий уровень формализации всех стадий расчета. Ошибки аппроксимации, обусловленные переходом к дискретному векторно-матричному описанию, полностью определяются характеристиками экстраполятора нулевого порядка вне зависимости от порядка объекта управления.

К недостаткам следует отнести: расчет параметров регулятора без учета влияния фазовой характеристики звена е"""; трудность применения такого подхода к разработке систем управления нелинейными объектами; зависимость всех коэффициентов, входящих в алгоритм вычисления управляющего воздействия на объект, от большинства параметров непрерывного объекта. Последнее обстоятельство значительно затрудняет перестройку параметров наблюдателя и регулятора, особенно если это необходимо производить в автоматическом режиме, реализация которого также возлагается на ЭВМ.

3.3. Структурный метод проектирования цифровых систем управления электроприводом

Анализ показывает, что применение различных методов проектирования цифровых систем приводит к различным системам разностных уравнений, реализуемых в ЭВМ. В связи с этим возникает проблема выбора метода, а следовательно, и системы разностных уравнений, наилучшим образом описывающих цифровую часть АСУ ЭП.

Область применения рассмотренных методов ограничена объектами, которые могут быть линеаризованы. При этом не учитывается влияние на динамику системы временного запаздывания между моментом определения текущего состояния объекта и моментом выдачи управления на объект. Кроме этого, к недостаткам рассмотренных методов можно отнести сложность перестройки получаемых дискретных алгоритмов управления.

В настоящем параграфе рассматривается структурный метод, основанный на представлении математического описания управляющей части АСУ ЭП, подлежащей реализации средствами ЭВМ, в виде детализированной структурной схемы аналоговой системы (ДСС). Ошибки, обусловленные реализацией непрерывных алгоритмов средствами цифровой техники, подразделяются на два типа. К ошибкам первого типа относятся ошибки дискретной аппроксимации непрерывных алгоритмов управления. Второй тип ошибок учитывает ошибки от преобразования цифрового сигнала в непрерывный и от наличия времени запаздывания Тм между моментами опроса датчиков состояния объекта и выработки управляющего воздействия.

Дискретная аппроксимация непрерывных алгоритмов управления, представленных в виде детализированных структурных схем, осуществляется путем замены каждой операции непрерывного интегрирования соответствующей дискретной аппроксимацией. При этом аппроксимация каждого процесса непрерывного интегрирования может вносить свою часть в суммарную ошибку первого типа при аппроксимации всего алгоритма управления.

Чтобы обеспечить возможность компенсации ошибок первого типа, при структурном методе переход от непрерывного описания к дискретному выполняется путем замены каждой операции непрерывного интегрирования выражением

x(z) г-1 у/ 1 Сти/То N То -x (г) Гн /г Л Р Р / Т„ / .

Сти /г + (1-Сти /)

г- 1

(3.7)

вытекающим из структурной схемы на рис. 3.8, в которой для компенсации фазовых искажений, обусловленных характеристиками экстраполятора нулевого порядка с передаточной функ-