1- г

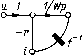Рис. 1.6. Структурные схемы звеньев автоматических систем: а - общая схема j-ro звена; б - структурная схема для уравнений вращательного движения; в - частный случай схемы j-ro звена; г - структурная схема н граф нелинейной электромагнитной цепи

ПОД знаком производной) со. Полагая z = fi (о), и) - (о)), откуда 0) = (1/Ур) 2, приходим к структурной схеме, изображенной на рис. 1.6, б.

Во многих случаях выходная координата звена, будучи преобразована через «свою» нелинейную зависимость (xi), входит в правую часть в явном виде:

а, --~- = fi {Хи 1 Xi i, A:i+i, . . . , х„, Ui, • • . , и/, t) - at

~h (поэтому соответствует структурная схема, изображенная на рис. 1.6, в. Примером такой записи может служить уравнение нелинейной электромагнитной цепи

u=ir-{-W

где Ф = / (О - магнитный поток; W я г - число витков и активное сопротивление цепи; и и t - напряжение и ток. Перепишем это уравнение в виде

и введем в рассмотрение обращенную кривую намагничивания, записав нелинейную зависимость, связывающую Фи/, следующим образом: i = f- (Ф). Отсюда

2 = м-г/-1{Ф); Ф(1/1Гр)2,

в результате чего приходим к структурной схеме, показанной на

рис. 1.6, г.

Особенностью приведенных выше структурных схем, соответствующих уравнению (1.11), является то, что они состоят только из простейших, элементарных звеньев - интегрирующих и безынерционных (к последним относятся как линейные - суммирующие и масштабирующие, так и нелинейные звенья, характеризующие функциональные зависимости). Такие структурные схемы - отдельных звеньев и системы в целом - получили название детализированных [15, 23]. Говоря более строго, детализированная структурная схема (ДСС) - это алгебраизированная математическая модель, состоящая только из элементарных звеньев (интегрирующих, дифференцирующих и безынерционных, в том числе нелинейных) с полностью вскрытыми связями между ними. Если в ДСС есть дифференцирующие звенья, то она с помощью структурно-топологических преобразований всегда может быть приведена к эквивалентной ДСС, состоящей только из интегрирующих и безынерционных звеньев.

Структурные схемы, в частности ДСС, представляют собой наиболее распространенный вид структурно-топологических моделей [22, 88]. Другим видом математических моделей этого класса являются сигнальные графы. Они представляют собой направленные взвешенные графы, т. е. их ветви характеризуются как определенным направлением, так и приписываемым им весом, или передачей. Этим они похожи на структурные схемы. Как графическое изображение сигнальный граф является более компактной моделью. Это хорошо видно из сравнения ДСС и сигнального графа электромагнитной цепи, изображенных на рис. 1.6, г. Вместе с тем структурную схему отличает более четкое различие таких элементов, как сумматор и отвод, переменная и передача. В табл. 1.1 иллюстрируются различия в графическом изображении элементов структурной схемы и сигнального графа.

Кроме основных правил структурных преобразований, которые могут быть использованы как для нахождения общей передаточной функции системы, так и для приведения ДСС (графа) к виду, удобному для исследования на ЭВМ и других целей, теория графов наряду с известными в теории управления преобразованиями линейных структурных схем [10, 63, 69] содержит дополнительные правила, такие как направленное нормирование детализированной структуры, теорема о некасающихся контурах (правило Мей-сона), правило инверсии. Все они рассматриваются ниже.

Применение относительных единиц и направленное нормирование. В теории автоматического управления широко распространены математические модели в относительных единицах. Переход к системе относительных единиц (нормирование) дает преимущества. Прежде всего, при этом существенно сокращается число коэффициентов в математическом описании системы, а сами параметры нормированной модели приобретают однотипность: для линейных звеньев - это базовые постоянные времени и безразмерные ко-

Таблица 1.1

Элемент

Переменная

Передача: линейный оператор нелинейный оператор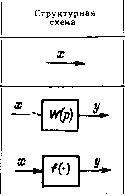

Сигнальный граф

Сумматор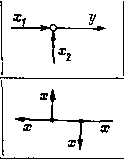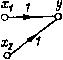

Отвод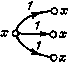

эффициенты усиления, для нелинейных - базовые постоянные времени и безразмерные статические характеристики (или их семейства). Как будет показано в дальнейшем, эти обобщенные параметры имеют вполне определенный физический смысл и могут быть определены экспериментально, что имеет большое значение для построения адекватной математической модели. Важно также и то, что в нормированном виде оказывается возможным сравнивать системы, элементы которых отличаются по номинальным данным, поскольку рассматриваются не абсолютные, а относительные изменения переменных. Заметим также, что описание автоматической системы в виде нормированной структурной схемы наглядно, имеет универсальный характер и облегчает комплексное исследование системы как графическими и частотными методами, так и путем моделирования на аналоговых вычислительных машинах (7, 22-26].

Как известно, относительным значением некоторой переменной называется отношение ее абсолютного значения к некоторому постоянному числу - так называемому базовому значению этой

переменной, т. е. 20

Х = х/Хб.

(1.14)