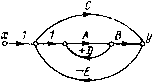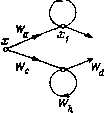£ *

jJr л, ж, г

Рис. 1.10. К использованию правила Мейсона

Правило некасающихся контуров (теорема Мейсона) является общим способом, позволяющим быстро определить передаточную функцию (передачу) между двумя любыми переменными структурной схемы (графа). Геометрическая интерпретация этого правила связана с понятием пути и контура, которые следует уточнить применительно к структурным схемам.

Путь - непрерывная последовательность направленных звеньев между двумя переменными, в которой ни одна из переменных не встречается более одного раза. К примеру, на структурной схеме н соответствующем графе, изображенных на рис. 1.10, «, между перем,енными л: и г/ - два прямых пути с передачами АВ и С.

Контур - замкнутый путь. На рис. 1.10, а структурная схема (граф) содержит три контура с передачами AD, - ABE и - СЕ (знак «минус» учитывает наличие отрицательной связи).

Некасающийся контур - контур, не имеющий ни одной общей переменной с другим контуром или путем. На рис. 1.10, а - два не касающихся друг друга контура с передачами AD и -СЕ, к тому же контур AD не касается прямого пути с передачей С. Если видоизменить эту структурную схему таким образом, чтобы на вход блока с передачей С подавалась та же переменная х-, что н на вход блока с передачей А, то такая схема не будет содержать некасающихся контуров, так как переменная х- в этом случае будет общей для всех контуров.

На основе правила Мейсопа в его геометрической интерпретации передача между любым входом хх и любым выходом Хвых

структурной схемы может быть составлена следующим образом:

Z [».пр(Р)Д(Р)1 W {n) = Jsiid£}- -, (1.20)

где Ар = I - I (р) + 2 (р) - 2 (р) + \ "EWkiip) - сумма передач всех контуров; Wk2 (р) - сумма произведений передач не касающихся друг друга пар контуров; S Wk3 ip) - сумма произведений передач не касающихся друг друга троек контуров и т. д.; Wtnp (р) - передача i-ro пути от

АГвх к ЛГвых; А,- (Р) = 1- 2 Wi,, ip) + 2 Wi,, ip) ~Wi,s ip) +

+ . . .; здесь S Wci - сумма передач контуров, не касающихся t-ro пути; 2 Fits (р) - сумма произведений передач всех пар контуров, не касающихся t-ro пути и друг друга; 211*3 (р) - сумма произведений передач всех троек контуров, не касающихся t-ro пути и друг друга и т. д.

В соответствии с этим выражением для структурной схемы на рис. 1.10, а аередаточная функция по управлению х равна

W (р) = У <Р) = Лб-f С(1-Р)

X (р) 1 - (AD - ABE - С£) + AD (-СЕ)

В частном случае, характерном для многих систем автоматизированного электропривода с одним усилителем, на входе которого суммируется несколько сигналов, и когда структурная схема обычно не содержит некасающихся контуров, передача определяется особенно просто - как сумма передач всех прямых путей 2 Wi пр (р), деленная на разницу между единицей и суммой передач всех контуров 2 W,i ip).

Если структурная схема или граф содержит несколько параллельных каналов (рис. 1.10,6), то правило некасающихся контуров может быть применено к каждому каналу в отдельности с последующим суммированием полученных передаточных функций. Как следует из правила Мейсона, петля с передачей Wf может быть интерпретирована как последовательное звено с передачей 1/(1-IF,) (рис. 1.10, в).

Во многих случаях нахождение передаточной функции системы путем преобразования ее структурной схемы превращается в громоздкую процедуру, тогда как применение теоремы Мейсона быстро приводит к результату. Рассмотрим, например, структурную схему, изображенную на рис. 1.11, а. Она содержит один путь от л: к г/ с передачей WWWb и три контура (они указаны стрелками) с передачами - WW, - WaWi и WiWb, причем контур 2 является некасающимся по отношению к контуру / и к прямому пути. После краткого анализа можно записать передаточную функцию в соответствии с формулой (1.20)

iWWb (1 + WWj)

Рис. 1.11. Примеры использования правила Мейсона

Поучительно рассмотреть систему с двумя входными воздействиями. Для схемы рис. 1.11, б знаменатели передаточных функций по управляющему воздействию х и возмущающему воздействию z получаются одинаковыми, так как они зависят только от передач контуров. Числители же получаются разными, поскольку различными являются пути от X я Z к у (или к любой другой переменной) и схемы касания контуров и путей. Так, для передаточной функции по управлению все контуры касаются единственного пути, имеющего передачу kl{Т{Гзр), которая и является, таким образом, числителем этой передаточной функции. Для передаточной функции по возмущению контур 3 с передачей - {/{TiTip") не касается пути с передачей - \l{fap), вследствие чего числитель передаточной функции имеет вид (- МТр) [1 + ХТТр)].

Применять правила некасающихся контуров нужно внимательно, чтобы не пропустить какой-либо путь или контур. В рассмотренном примере при нахождении передачи, например, от 2 Ух кроме пути по направлению контура 2, имеется еще один путь - по контуру / к переменной г/а и далее по контуру 3 к конечной переменной у.