нием kit) = А (t) X (О + В {t) u it), называется полностью управляемой, если она может быть-переведена из произвольного начального состояния Хо = X (о) в произвольное конечное состояние Xj = x(/i) в течение конечного промежутка времени t-to при помощи ограниченного управления и (О, to t t.

Для линейной стационарной системы, описываемой уравнением (1.37), проверка факта управляемости осуществляется наиболее просто. Для этого необходимо составить так называемую матрицу управляемости Р = (В, АВ, АВ, . . . , А"~ В). Эта матрица имеет блочную структуру: ее элементами являются также матрицы - В, АВ, АВ и другие (общим числом п), каждая размером п X т, поэтому матрица Р имеет п строк и тп столбцов. Необходимым и достаточным условием полной управляемости системы (1.37) является равенство ранга матрицы Р порядку системы: rank Р = «. Напомним, что рангом матрицы называется наивысший порядок отличных от нуля миноров этой матрицы (т. е. всевозможных определителей, составленных из элементов, стоящих на пересечении выбранных строк и столбцов матрицы).

Поясним сказанное примером. Пусть имеется объект с одним входом, структура которого изображена на рис. 1.20, а матрицы "А и В имеют вид

ГО Oi 1 ГО 1

А= ; В=

требуется исследовать управляемость объекта и рассчитать модальный регулятор таким образом, чтобы система имела характеристический многочлен

Я»(р) = р + 2«оР+юо,

где ©о - константа, определяющая быстродействие системы. Определим сначала матрицу управляемости. Находим

(ai>0; а2>0).

,012

l-ah

Р = (В, АВ)

Ранг матрицы Р равен двум, так как определитель второго порядка det Р отличен от нуля. Следовательно, данный объект по входу U полностью управляем, и, значит, может быть построен модальный регулятор, реализующий любую заданную динамику.

Поскольку объект - второго порядка и имеет один вход, то матрица обратной связи к является строкой с элементами ki и (это вытекает из необходимости согласования размеров матриц А, В и к, как видно ниже). Тогда

/7, 1 гП 1

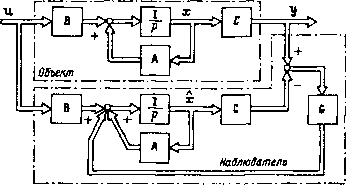Рис. 1.20. Замкнутая система наблюдения

Далее должно выполняться равенство

L «2(1 + 1) Р + а,{1 +h) J

det (pi-А)-

= р* + 2©ор + а)о.

Раскрывая определитель и приравнивая коэ4х})ициенты при одинаковых степенях р, получаем два алгебраических уравнения, из которых определяются искомые коэффициенты обратных связей

- 1;

1.

Реализация линейной обратной связи по состоянию часто бывает затруднена тем, что не все координаты объекта, т. е. составляющие вектора состояния, доступны непосредственному измерению. Однако во многих случаях удается построить устройство, называемое наблюдателем, вырабатывающее оценки тех координат объекта, измерение которых осуществить нельзя. Для объекта, описываемого уравнениями

x = Ax--Bu; у = Сх, уравнение состояния наблюдателя имеет вид

x = Ax-f Bu-f G(y-у).

(1.40)

(1.41)

где у = Сх; О -произвольная постоянная матрица. Из этого уравнения и соответствующего ему рис. 1.20 видно, что входами наблюдателя служат входы и измеряемые выходы объекта. Совместно решая уравнения (1.40) и (1.41), получаем уравнение ошибки оценивания

X-х = (А-ОС)(х-х).

Известно, что если собственные числа матрицы А-GC, т. е. полюсы системы объект-наблюдатель, лежат в левой полуплоскости, то при -> оо ошибка оценивания х-х -> О, т. е. переменные состояния наблюдателя асимптотически сходятся к аналогичным переменным объекта и, таким образом, являются их оценками. Скорость сходимости оценок координат к их истинным значениям зависит от расположения полюсов системы объект - наблюдатель. Поэтому важно иметь возможность выбирать эти полюсы по своему усмотрению. Воз.можность построения наблюдателя и произвольного размещения полюсов определяется важным свойством систем, называемым наблюдаемостью.

Система

х(/)=-А(/)х(0-гВ(Ои(0; у(0 = С(г)х(0

называется полностью наблюдаемой, если для всех можно единственным образом определить х(о) по данным измерения и (t) и у (t) на конечном интервале времени /ц i- Для линейной стационарной системы (1.40) необходимым и достаточным условием патной наблюдаемости является условие rank Q = л, где матрица наблюдаемости Q = 1С\ АС, (А-УО , . . . , (А)"- О].

Нетрудно убедиться, что если в рассмотренном нами примере измеряемой координатой является Xj, то объект по этой координате полностью наблюдаем, и, следовательно, может быть построен наблюдатель с желаемым размещением полюсов. На рис. 1.21 показана реализация модального управления для случая, когда одна координата объекта Xi непосредственно из.меряется, а другая х

Объект

Наблюдатель