РаширенныЛ оВьпкт

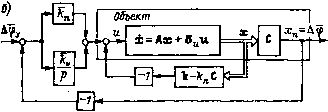Рис. 5.7. Структурная схема системы управления положением: а - с введением интеграла; б - с интегрирующим регулятором положения; в - с пропорционально-интегральным регулятором положения

Однако соответствующая такому описанию схема, приведенная на рис. 5.7, а, где - коэффициент передачи интегральной связи на практике не может быть реализована из-за необходимости располагать не только абсолютным значением угла, но и интегралом от него.

Существуют два варианта возможной реализации следящего электропривода при введении интеграла в закон регулирования:

l.Jia вход интегратора kjp подается ошибка рассогласования 6ф = фу-ф (рис. 5.7, б). Необходимость введения обратной связи по абсолютному значению угла (р ~ Хп в этом случае сохраняется.

2. Обратная связь по углу с коэ4х})ициентом k„ включается в прямой канал, а регулятор состояния описывается матрицей-строкой (к-knC) (рис. 5.7, в). Благодаря этому получается классический ПИ-регулятор положения с передаточной функцией

Тр. пР +1

Wp.„ip) =

knP + *и

Рр.п

Тр. пР

где Рр.п = п; Тр,п = kn/kn, И МОЖНО говорить о следящем элек-

троприводе с подчиненной подсистемой управления скоростью исполнительного органа.

Вне зависимости от варианта реализации характеристическое уравнение замкнутой системы записывается как

det[pl-А-В; [к/г„]]=0.

Однако динамические свойства систем (рис. 5.7, бив) при уп- • равлении оказываются различными. В первом варианте нормированная передаточнай функция, связывающая ф с фу, определяется как

1Гз(р,)= 1/Р(р), (5.3)

где Р (р) = р"~ + /ip" + . • • + fnp* + 1, благодаря чему характер изменения управляемой переменной однозначно определяется распределением корней характеристического уравнения. Недостатком является то, что порядок астатизма системы по управлению получается равным единице, в результате чего может оказаться невозможным обеспечить требуемые показатели при отработке управляющего воздействия. Во втором варианте порядок астатизма повышается до двух, но при этом приходится считаться с тем, что на вид переходной характеристики влияет нуль передаточной функции, которая получается в виде

ia(p*) = (f„P*+l)/P(p*). (5.4)

Учитывая удобство способа определения параметров регулятора, основанного на использовании стандартной формы распределения корней, целесообразно воспользоваться им и для определения параметров регулятора в контуре положения.

Скоростная подсистема, описываемая уравнениями (5.1), представляет собой систему высокого порядка, что делает почти невозможным получение результата в общем виде. Учитывая, что характер изменения скорости ИО при управляющем воздействии в скоростной подсистеме, замкнутой через наблюдатель, получается близким к характеру изменения выходной координаты модели в системе, описываемой уравнениями (5.2), будем при определении требуемых параметров регулятора положения считать, что скоростная подсистема представляет собой двух- или трехмассовую рядную систему, замкнутую по вектору состояния механизма. Если, кроме того, пренебречь влиянием малых постоянных времени, то можно считать, что скоростная подсистема описывается передаточными функциями третьего или пятого порядков, а порядок уравнений, характеризующих следящий электропривод с ПИ-регулято-ром положения, будет пятым и седьмым соответственно.

В практике проектирования жестких следящих систем щироко используется настройка контура положения на симметричный оп-

Таблица 5.2

Порядок

Коэффициенты, обеспечивающие перерегулирование, равное 40к, при применении ПИ-регулятора положения

тимум (СО), при которой перерегулирование по управлению составляет примерно 43 %. Передаточная функция контура, настроенного на СО, получается по формуле (5.4) при л + 1 = 3 и распределении корней по Баттерворту. Проведенные расчеты позволили получить значения коэффициентов полинома Р (р), при которых перерегулирование по положению составляет около 40 % и при более высоком порядке характеристического уравнения, а колебательность внутренней системы, описываемой передаточной функцией

,..п-1

(5.5)

соответствует таковой при распределении ее полюсов по Баттерворту. Значения коэффициентов при л + 1 = 3 8 для предлагаемой стандартной формы в виде

P»(p)=p"* + fiCOoip" + f2«oV~+ . . . +Wp + cuo"i+, (5.6)

где - среднегеометрический корень (СГК), характеризующий быстродействие системы, замкнутой по положению, приведены в табл. 5.2, а реакция на скачок управления Афу при л + 1 = = 3 -г- 10 - на рис. 5.8.

Записывая передаточную функцию разомкнутой системы для схемы на рис. 5.7, в в виде

(5.7)

Wip) = h.„ + 0.3(р)-

Тр. пР

где Wj, (р) определяется выражением (5.5), при коэффициентах а,-, соответствующих распределению Баттерворта третьего или пятого порядка (соответственно для двух- и трехмассовой системы), и приравнивая полученный с учетом этого выражения знаменатель передаточной функции (5.4) стандартному полиному Р" {р)/(л+\ можно определить, что для системы с двухмассовым механизмом средне-