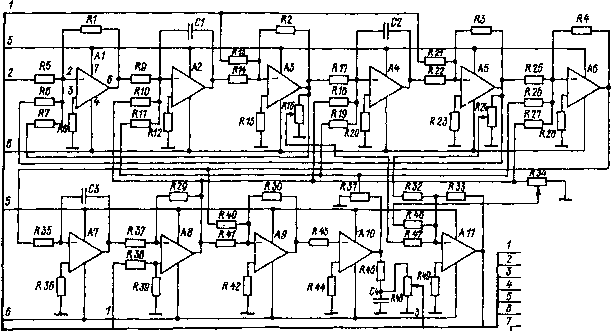
Рис. 8.9. Функциональная схша адаптивно-модального регулятора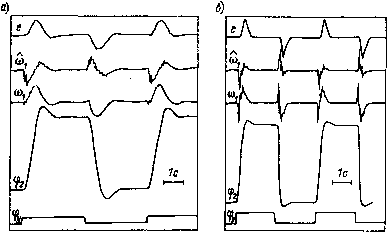

Рис. 8.10. Реакция следящей системы с упругостью на прямоугольное задающее воздействие: а - исходная система; б - система с AMP

тивной системы обратная связь по скорости двигателя размыкается и на вход регулятора скорости подаются выходные сигналы AMP.

На рис. 8.10, а показана реакция исходной следящей системы с упругой связью (с коэффициентом соотношения масс у = 35, характерным для некоторых безредукторных приводов) на ступенчатое задающее воздействие фу с амплитудой ± 5°. На осциллограмме показаны сигналы, соответствующие переменным фу, фг, ©i (выход тахогенератора), ©i и е = фу--фг. Система настроена так, чтобы упругие колебания не возбуждались. Переходная характеристика по положению механизма фг имеет перерегулирование о = 13 %, время нарастания (первого достижения установившегося значения) = 0,7 с, время регулирования /р = 1,6 с. В следящей системе с AMP переходная характеристика (рис. 8.10, б) имеет, показатели качества 0 = 5%, ti= 0,3 с и tp = 0,6 с. Существенного повышения быстродействия удалось достичь в результате гашения адаптивно-модальным регулятором упругих колебаний в системе. При введении на вход регулятора скорости сигнала адаптации следящая система, как показали эксперименты, оказывается почти нечувствительной к изменению контурного коэффициента передачи контура скорости в пять и более раз (например, при изменении коэффициента передачи регулятора скорости) и к изменению момента инерции механизма в три и более раз. В качестве примера на рис. 8.11 показаны осциллограммы переходных процессов в исходной и адаптивной системах при отработке ступенчатого изменения заданного значения (± 5°) в нормально настроенной системе и после 2,5-кратной расстройки значения коэффи-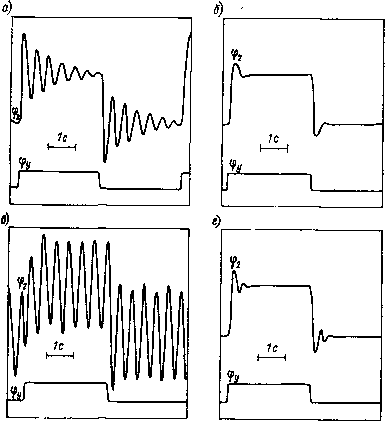

Рис. 8.11. Реакция следящей системы с упругостью на прямоугольное задающее воздействие при нормальном (а, б) и увеличенном в 2,5 раза (в, г) значении коэффициента передачи регулятора скорости: а, в - исходная система; б, г-адаптивная система

циента передачи регулятора скорости. Осциллограммы отчетливо иллюстрируют эффект стабилизации характера переходного процесса адаптивным регулятором.

Эффективность регулятора была проверена на стенде также при работе его в составе следящей системы с жестким объектом, имеющим зазор (2фо = 3°). На рис. 8.12, а показана реакция исходной системы с V = 30 и добротностью, равной 20, на прямоугольное задающее воздействие с амплитудой ± 5°. Наблюдаются медленно затухающие колебания вала механизма. Включение AMP приводит к ликвидации этих колебаний (рис. 8.12, б) при сохранении добротности.