определить оригинал, представляющий собой зависимость ско-> рости Дсог от времени:

.де kcTj{2-yJy Ту) - коэффициент демпфирования звена вто-

,pofo порядка в знаменателе передаточной функции {р)1 i(p)-При слабом механическом демпфировании (при Ъ, 1) выражение для Да)2(0 упрощается:

Дша (0~ехр/ -

( v7rj

ч VyTy ) V Vy Ту Таким образом, угловая частота колебаний второй массы при заторможенной первой равна \/{л/уТу), а затухание этих колебаний определяется значением la-

При изменении момента двигателя движение ИО будет определяться передаточной функцией

Приложив кратковременно момент к первой массе (например, подключив на короткое время двигатель к источнику питания), можно вызвать колебания всей двухмассовой системы. Считая, что изменение момента имеет характер единичной импульсной функции Л1д {t) ~ 8 {t), .можно записать

Дсо2 (0 =

или при и « 1

1 -ехр I -

£2 «12

1. ехр(-

6(0-

Постоянную времени Гу называют постоянной вре.мени упругих колебаний двухмассовой системы. Затухание колебаний определяется коэффициентом демпфирования = kcTj{2Ty).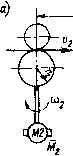

FyyCp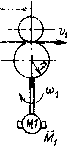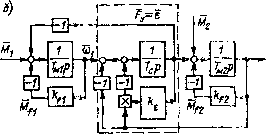

(O2 А<й/

Рис. 2.4. Двухмассовая электромеханическая снсте.ма с упругостью втор.згс рода: а - функциональная схема; б - нелинейная структурная схема; в элемент линеаризованной структурной схемы

При замкнутой на источник питания якорной цепи колебани* скорости двигателя и его ЭДС вызывают колебания тока якоря и момента /Ид. Это оказывает демпфирующее воздействие на процесс колебаний в электромеханической системе.

Будем называть двухмассовые электромеханические системы, в которых упругим звеном является кинематическая передача, свя зывающая двигатель с исполнительны.м органом, системами с уп ругостью первого рода.

На рис. 2.4, а показана схема механизма с упругостью второго рода, в которо.м упругим элементом является транспортируемый или обрабатываемый материал (бумажное полотно, ткань, Kop.i и т. п.); Ml и М2 - двигатели первого и второго валов, которые могут работать как оба в двигательно.м, так и Ml ~ в двигательном: а М2 - в тормозном режиме. Радиусы и могут быть постоян ными, если это радиусы валов механизма, или меняться в процессе работы, если это радиусы перематываемых рулонов.

Составим структурную схему такого звена при следующих допущениях:

а) материал однороден и имеет по всей длине одинаковую тол щину и ширину;

б) влиянием массы материала на его деформацию можно пренебречь;

в) деформация имеет чисто упругий характер, причем равномерно распределяется по поперечному сечению материала;

г) волновыми процессами, связанными с распределениями деформации по длине, можно пренебречь.

Поведение материала на участке растяжения длиной / описывается дифференциальным уравнением [42, 91 ]

- .{1 е)

dt I " I

где е - относительное удлинение; Vi и - линейные скорости в начале и конце участка растяжения /.

Натяжение, возникающее в материале, связано с абсолютным значением растяжения А/ выражением Fy = СрД/ = Ср/е. Подставляя сюда значение е и записывая уравнения моментов для двигателей, можно получить уравнения, характеризующие рассматриваемую систему:

е =-f.

у>

(2.11)

При переходе к относительным единицам выберем следующие соотношения между базовыми величинами: Уб = V26 = b>j6ri= «262 = Уб; Mi6 = М/16 = Fy. б г; М26 = М/2б = Fy.arf,

= Fy.6/(cp/). Эго позволяет непосредственно по исходной структуре перейти к НДС, параметрами которой являются постоянные времени Т, = Fy.eKcpVe); Ti = J lUiKJMio; Г„ 2 =/226/26 и безразмерные кож{)фициенты kg, = Fy.6/(СрО, kfi и kf-

Постоянная времени жесткости полотна Т. численно равна вре мени, за которое натяжение изменяется от нуля до базового значения при скачкообразном увеличении разности скоростей v-Vi и условном отсутствии поступления полотна в зону деформации. Трактовка физического смысла Тс имеет характер, общий для апериодического звена, а выражение постоянной времени жесткости аналогично выражению постоянной времени любого упругого звена с поступательным движением.

Нормированная детализированная структурная схема механизма приведена на рис. 2.4, б. Специфической особенностью упругого звена второго рода является характер демпфирования колебаний

Заказ J* 398 j55