* м2

с32 kc32

Aii ii = О

С32 ксз2

Tci2 Т„.

С, = [0 о 1]; Вт,=0; В„„ =

0 0 0 -

0 О

В объекте за входную координату принята скорость зеркала Аизер = Ай)з = Хт, поэтому

С,[ = [0 О О 1 О 0].

Ошибка восстановления выделяется как х-Хю при Сн = = [00 0 1]. Связь наблюдателя по ошибке восстановления рекомендуется вводить только на последний интегратор модели, приняв L = [О О О 1Г.

4. По уравнению (5.1) необходимо оценить реакцию системы на управляющее воздействие Аиу и возмущение в виде изменения момента нагрузки.

Требуемое значение коэффициента наблюдателя / следует определить в результате рассмотрения реакции скоростной подсистемы на ступенчатое изменение момента нагрузки на третьей массе, моделирующей зеркальную часть антенной установки. При / = О, т. е. когда система замкнута через модель, изменение момента нагрузки вызывает слабозатухающие колебания зеркала на частоте первого резонанса. При /> О эти колебания демпфируются и при / = 10 после первого отклонения скорости зеркала в кривой

Аиз/АМс = /(0 колебания почти отсутствуют. Дальнейшее увеличение / не приводит к заметному изменению характера реакции на возмущение, что дает основание рассматривать / - 10 как то минимальное значение, которое должно быть использовано при построении наблюдающего устройства.

В результате описанной процедуры значение = 13 c" определено как предельное. Значения коэффициентов регулятора при этом равны: 16,45;2 = - 11,5; кз = ~ 10,63; 4=29,16;

5 = 0,66. Расчетная реакция скоростной подсистемы, замкнутой

i I L-.L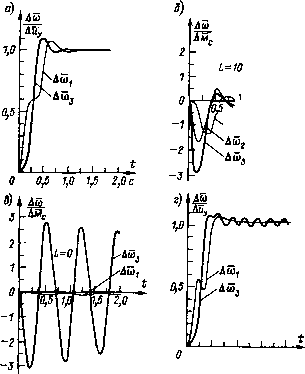

1,0 1,5 Zfl с

Рис. 5.6. Расчетные переходные процессы в скоростной подсистеме: а, б - реакция на скачок управления и возмущения в системе с наблюдателем иа базе трехмассовой модели при / = 10; в - при скачке возмущения и / = 0; г -- при скачке управления с наблюдателем на базе двухмассовой модели

через наблюдатель с / = 10, на скачок внешних воздействий показана на рис. 5.6, а и б. Рисунок 5.6, в иллюстрирует реакцию системы на воз.мущение при / = 0. Видно, что при замыкании по модели скорость двигателя почти не меняется при слабо затухающих колебаниях зеркала.

Аналогичным образом производились расчеты для системы с наблюдателем на базе двухмассовой модели (см. рис. 2.23). Предельное быстродействие системы характеризовалось при этом значением ©0=11 c". Коэффициенты регулятора получились равными ki = == 16,25; 2 = 15,16; = - 7,09. При том же значении I реакция системы на возмущение была близка к показанной на рис. 5.6, б. В кривой Ашз = f (t) (рис. 5.6, г) видны слабо затухающие колебания на частоте второго резонанса. Переходные характеристики по управлению близки к таковым при замыкании по координатам модели при / = 0.

5.3. Настройка контура положения следящего электропривода

Опорно-поворотные устройства крупных радиотелескопов оборудуются силовыми следящими электроприводами наведения, т. е. электроприводами с автоматизированной системой управления, замкнутой по положению исполнительного органа. Предусматривается внутренняя скоростная подсистема, при применении к которой изложенных выше принципов построения систем управления с упругостью, она представляет собой систему управления скоростью исполнительного органа.

Рассмотрим в общем виде вопрос о выборе параметров регулятора положения в следящем электроприводе с упругостью, предполагая, что скоростная подсистема замкнута по вектору состояния механизма.

Матричное уравнение объекта

X = Ах + ВаЫ

имеет порядок п на единицу больший, чем порядок уравнения скоростной подсистемы из-за того, что к координатам объекта добавляется новая регулируемая переменная в виде угла поворота ИО. Если регулятор положения - пропорциональный, то в результате наличия в структуре объекта интегратора, преобразующего скорость ИО в угол поворота, характеристическое уравнение следящего электропривода оказывается таким же как характеристическое уравнение системы управления скоростью с введением интеграла в закон регулирования. Поэтому сказанное в § 2.3 о выборе параметров регулятора при введении интеграла в закон регулирования справедливо и для следящего электропривода при коэффициенте регулятора положения численно равном fep.n = МТ, где Ти -постоянная времени интегратора И на рис. 2.10, а, определяемая в соответствии с последним выражением в формулах (2.27).

Как и для жесткой системы подчиненного регулирования, применение пропорционального регулятора положения обусловливает наличие угловой статической ошибки при изменение! момента нагрузки. С целью обеспечения астатизма системы при возмущении в закон регулирования должен быть введен интеграл от регулируемой переменной. Тогда при выборе параметров регулятора положения необходимо оперировать с расширенным объектом, описываемым матричным уравнением

х = Ах + В„ы,