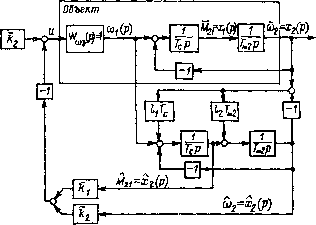Рис, 3.2. Упрощенная структурная схема аналоговой системы управления

скоростью с наблюдателем

Даже для такой, сравнительно простой системы, как показанная на рис. 2.23, преобразования и их результаты оказываются достаточно громоздкими. Поэтому для пояснения сказанного и получения обозримого результата в общем виде введем некоторые упрощающие допущения. Пусть у w 1. Тогда, как это следует из изложенного на стр. 98, контур регулирования скорости двигателя может быть замкнут так же, как в жесткой системе. Если при этом частота среза его ЛАЧХ существенно выще частоты упругих

колебаний исполнительного органа {л/уТу)~ ЦТТы, то при kc = О объект управления может быть представлен в виде рис. 3.2, где считается, что замкнутый контур скорости двигателя почти безынерционен. Для обеспечения плавного движения ИО вводятся обратные связи по скорости исполнительного органа и упругому моменту, восстанавливаемому наблюдателем. Тогда передаточные функции Wi (р) и Wi (р) могут быть представлены

в виде

Ц7,(р)=4р(

+ [(¥.7„2 + *2)/(7-с7„2)1р

Щ (р)

Wi {p)=Js -

Щ (Р)

1 + hp- + 1(Т„2 + 11)1{ТсТш)] Р-* (hk-r hh) + [(hh)ITui - ikkl)lTc] р-

И-гр-Ч-ИТ„2 + «/(г,г„а)1 р-»

где ki = 1,4(ОоТ,; = ПГ„з4-1; 1 = ТА -Г7; 1 = == 1,4 (Ооя- Значения ©о и ©он по-прежнему характеризуют быстродействие системы и наблюдателя.

Переход от непрерывного описания алгоритма управления к дискретному выполняется способом подстановки в tti (р) и W (р)

вместо р его дискретной аппроксимации вида Tozl{z-l). В результате, после преобразований, закон управления в дискретной форме можно представить как:-

и (г) kp. сЫу (z) -Uo. с (z); «о. с (2) = ai«o. с (2) 2-1 -айо. с (г) z + азЩ (z) ~ - 04©! (z) -f Gsffla (z)-йвЫг (2) 2-1 или в виде системы разностных уравнений:

uin+l) = kp,cUy{n+l)-Uo.c(n+ 1); «о, с (« + 1) = OiUo. с (п) - a2«o. с (п - 1) + йзЮ 1 (п + 1) - ~аф1 (п) + ащ (п -г 1)-ааа ("), где fli = (2 + IJoVN; = 1/Л;

«3 = [ТоТ„2 + 70 (/2iTm2 + )]/(П7„2Л); 4 = 7о/(ПЛ);

fle = 7-, (/А + khVN; N = l + Tok + To (Г„2 + hWcT).

Структурная схема системы с наблюдателем и регулятором, реализованными в цифровой форме на основе подстановочного метода, приведена на рис. 3.3. В этом случае алгоритм управления , уже не может быть разделен на отдельные части: наблюдатель и регулятор, поскольку разностные уравнения определены по общим передаточным функциям Wi{p) и (р). Все коэффициенты щ, входящие в описание алгоритма, в неявном виде зависят как "от параметров объекта, так и от коэффициентов наблюдателя - L и регулятора - к. Следовательно, изменение любого из параметров системы требует пересчета всех коэффициентов алгоритма управления. Кроме этого, к недостаткам подстановочных методов следует отнести то, что при проектировании наблюдателя и регулятора не учитываются характеристики ЦАП и звена чистого запаздывания.

wJz)

Рис. 3.3. Структурная схема цифровой системы с наблюдателем 8* 115

3.2. Проектирование цифровой системы управления по дискретному векторно-матричиому описанию объекта

Рассматривая второй подход к проектированию АСУ ЭП, обратимся к системе, замкнутой по принципам модального управления. Пусть объект управления порядка п со скалярным входным воздействием описывается матричными уравнениями:

(3.1)

где А - квадратная матрица объекта размером л X л; В - матрица управления п X 1; С - матрица выхода 1 X г; г - число измеряемых переменных.

Известно [491, что решением уравнения (3.1) является

X (О = Ф (О X (0) + S Ф (-т) Вы (/) dT, о

(3.2)

где Ф {t) = е* - переходная матрица объекта.

При переходе к дискретной аппроксимации непрерывного объекта (рис. 3.4, а) считается, что входной сигнал квантуется с периодом дискретности Г,, а затем преобразуется экстраполятором нулевого порядка. Выполнение этого условия означает, что входной сигнал остается постоянным в течение n-vo такта квантования, т. е. и (/) = и{пТо), при пТа< t {п + 1) Т.

Уравнение состояния объекта в этом временном интервале при ненулевых начальных условиях х (лГо) в соответствии с решением (3.2) будет определяться выражением

X (О - Ф (/ - лГо) X («Го) -f и (пТо) S Ф (/ -т) BdT.

ff) u(z)

x(z)

Рнс. 3.4. Дискретная аппроксимация непрерывного объекта (а), векторно-матричная структурная схема (б)