Ofi 0,5 0,6

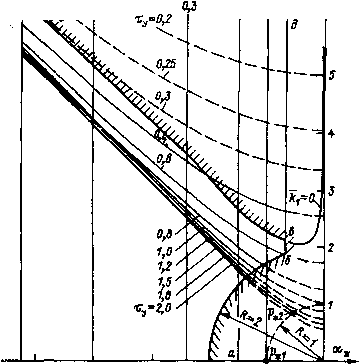-5 -3 -Z -7 0

Рис. 2.12. Область допустимых соотношении параметров на плоскости корней

Выбирая ДЛЯ настройки на оптимум по модулю кр,с = TJ(2Tj3), получим, что полюсы системы распределяются по Баттерворту при соо = а нормированная передаточная функция имеет вид

pi + 2р2 + 2я. + 1

Как показывает опыт эксплуатации систем подчиненного регулирования, их чувствительность к изменению tjs является вполне приемлемой на практике. Исходя из этого целесообразно потребовать, чтобы чувствительность рассматриваемой упругой системы к изменению Гэ была не выше, чем в жесткой системе. Сравнительный анализ чувствительности передаточных функций Wza (р) " 3 ip) показывает, что чувствительность системы к изменению х, замкнутой повектору состояния, будет практически такой же,

гкак в жесткой системе, если неуправляемый корень р будет располагаться не выше линии вг, являющейся частью линии = О, построенной на основании выражения (2.24) для ki. Это дает основание принять линию 1 = О за верхнюю границу области допустимых соотношений параметров, ограниченной кривой абвг (на рис. 2.12 заштрихована с внешней стороны).

Для оценки возможного быстродействия системы и выбора его в зависимости от соотношения постоянной времени упругости Ту и эквивалентной малой постоянной времени Гэ удобно область допустимых соотношений параметров строить в координатных осях т/ту, Ту или, что то же самое, Тэ/Ту, Ту. Кривая абвгО, ограничивающая эту область, показана сплошной линией на рис. 2.13.

На основании выражения (2.21) для Wtou (р*) может быть записано выражение переходной характеристики для скорости дви-

• гателя:

где т = /С0(,; f (т) - переходная характеристика, соответствующая передаточной функции р/{р + 2р + 2р + 1). Кривая f (х) при Тэц = О показана на рис. 2.11. Поскольку к моменту достижения ею максимума приращение (т)/Д(Вуст еще пренебрежимо мало, значение /max характеризует отнесенный к установившемуся приращению бросок скорости двигателя в начале переходного процесса при ступенчатом управляющем воздействии

\ Дшуст /

= 0,31уту.

WycT /max

Переходные характеристики to а (т), близкие к соответствующим настройки Баттерворта, могут быть реализованы при условии, что для этого не требуется недопустимо большого значения начального броска скорости двигателя, а следовательно, и тока якоря. В левой части рис, 2.13 сплошной линией показана зависимость %.пред = f (у), соответствующая броску скорости двигателя, равному ее установившемуся приращению (Аа JА(»у„)= 1, что обычно допустимо при использовании двигателей общепромышленного назначения.

На основании изложенного рекомендуется следующий порядок расчета системы, обладающей наибольшим возможным быстродействием:

1. По известному значению Т/Ту на основании графика рис. 2.13 определяется значение Ту, при котором характеризующая точка лежит на верхней границе области допустимых соотношений параметров с учетом значения Ту.пред, определенного по у.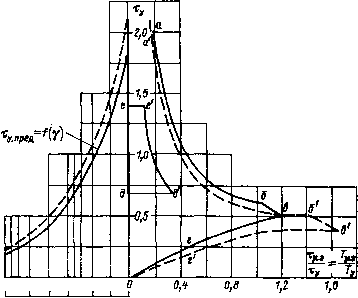

уЮО W 20 10 4 2 1

Рис. 2.13. Номограмма для оаределения возможного быстродействия системы, замкнутой по вектору состояния механизма

-- система без введения интеграла; --- - с введением интеграла

2. По выражению Шо = Ту/Гу определяется средний геометрический корень, характеризующий максимально возможное быстродействие системы.

3. Рассчитываются относительные постоянные времени тэ = = Гр,эСОо и т„ = Г„СОо.

4. По формулам (2.24) вычисляются коэффициенты регулятора Ai, ki и Аз.

Передаточные функции системы по возмущению, записанные на основании выражения (2.17) с учетом того, что и = кхц, получаются в виде

ДМс (р.)

(p»)

ДлТс (р.)

=(-1)

Тм2= (-1)

pijApl+Bpl + Cp+d Я (р.)

fpl + Gp, + k Н (Р.)

(2.25)

где Я (р*) = Я* (р) - характеристический полином, определяемый выражениями (2.22) и (2.23);