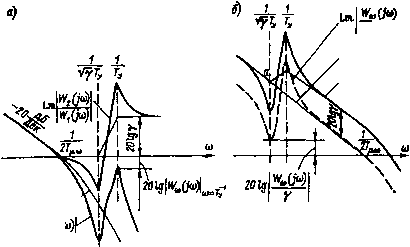ИСИ1

Рис. 2.9, К оценке влияния упругости на контур скорости

влиянием упругости на контур скорости может оказаться возможным:

1) частота упругих колебаний значительно выше частоты среза ЛАЧХ контура скорости (рис. 2.9, а);

2) быстродействие контура скорости настолько велико, что сравнительно низкочастотные колебания упругого момента ие приводят к колебаниям скорости двигателя (рис. 2.9, б).

В первом случае, считая в соответствии с.постановкой задачи, что коэффициент пропорционального регулятора скорости выбран из расчета получения в жесткой системе передаточной функции разомкнутого контура W° ip), соответствующей настройке на РМ, получим, что в области частот, больших частоты среза жесткого контура ft)c = 1/(27ци), фазовая характеристика пересекает линию -180°. В случае когда появившийся в результате влияния упругости резонансный всплеск амплитудной характеристики Lm I (/со) I на частоте \/Ту поднимается выше оси частот, система оказывается неустойчивой. Влияние упругости будет пренебрежимо мало, если выполняется неравенство20 Ig \ W{ja>)\j.-\ < -6дБ

и если Lm tto,(/co) мало отличается от Lm W° (/«) в зоне частоты среза. Будем считать, что и в области частоты 1/Ту частотная характеристика контура скорости, настроенного на ОМ, в жесткой системе описывается выражением

WT (/со) =---,

где Гц, - суммарная малая постоянная времени контура скорости.

Тогда на основании выражения для (р) выражение для амплитуды частотной характеристики при резонансной частоте получится в виде

где врэ = TJTy. Для пренебрежения упругостью необходимо выполнение условия W„ (/со) < 0,5. Если в области ча-

стоты 1/Ту характеристика жесткой системы идет круче, чем это определяется принятым выражением для W° (/со), то при выполнении этого неравенства сформулированное требование будет удовлетворяться с запасом.

Чтобы характеристика контура скорости при частоте среза мало отличалась от Lm j W"" достаточно потребовать, чтобы соблюдалось соотношение постоянных времени лJyTy < Т. Тогда в самом худшем случае это отличие при ш = 1/(2Ги) не будет превышать -2,5 дБ. Поскольку в рассматриваемой области частот характеристики контуров, настроенных на ОМ и СО, совпадают, сказанное справедливо и при настройке системы на симметричный оптимум.

Во втором случае (рис. 2.9, 6) частота среза ЛАЧХ контура скорости, настроенного на ОМ, выше частоты 1/Гу. Амплитуда ЛАЧХ Lm (/<»)/Wi (/со) в области высоких частот равна 20 Ig у. Поэтому, чтобы сохранить в зоне частоты среза вид ЛАЧХ контура скорости с упругостью таким же, как в жесткой системе, надо снизить коэффициент усиления регулятора скорости kp,c в у раз по сравнению со значение.м, соответствующим настройке по ОМ. Логарифмическая амплитудная частотная характеристика в зоне частоты среза будет мало деформироваться, если Ту > 2{2Т).

При выполнении этих условий для пренебрежения упругостью надо, чтобы выполнялось условие:

. . , > 6 дБ.

Если стремиться настроить контур скорости на оптимум по модулю, то это сведется к требованию

e,эV[(v-l) + 4vgЫ(eз + v)

Возможность настроить контур так же, как в жесткой системе, не означает, однако, возможности пренебрежения влиянием упругости на работу системы, так как необходимо еще оценить характер изменения скорости исполнительного органа Wj. В первом слу-

чае резонансный всплеск характеристики, соответствующей передаточной функции Дсог (р)/Дсо1 (р), будет практически компенсирован за счет провала ЛАЧХ Lm \Wa{}(s))\ при частоте И(л/у Ту) (см. рис. 2.9, а). В характеристике, связывающей скорость исполнительного органа с задающей величиной на входе контура скорости, будет существовать резонансный всплеск при частоте ИТу. Однако, поскольку он будет располагаться значительно ниже оси абсцисс, амплитуда колебаний исполнительного органа будет невелика.

Во втором случае, а также при у 1 скорость двигателя меняется, как в жесткой системе при стандартной настройке, электропривод практически не будет демпфировать колебания исполнительного органа на резонансной частоте 11{-\/уТу), и они будут затухать только под действием сил трения. В этом случае так же, как в случае, когда параметры системы таковы, что влиянием упругости пренебречь нельзя, возникает задача выбора настроек регулятора, а, если это необходимо, то и применения специальных способов коррекции, которые позволили бы обеспечить плавное движение ИО при максимально достижимом быстродействии системы.

2.3. Двухмассовая электромеханическая система, замкнутая по вектору состояния механизма

В предыдущем параграфе рассматривалась система, внещний контур которой представляет собой контур регулирования скорости двигателя. Однако существует принципиальная возможность при сохранении внутреннего токового контура, что позволяет осуществлять управление током якоря, реализовать внешние связи не только по скорости двигателя, но и по скорости исполнительного органа и упругому моменту.

Функциональная схема замкнутой по вектору col [coAf aiWg] системы управления скоростью с подчинешгым токовым контуром показана на рис. 2.10, а. Поскольку (Oj, М21 и «а являются координатами механизма, можно говорить, что замкнутая таким образом система замкнута по вектору состояния механизма. Для выделенного тонкой линией объекта внешними воздействиями являются сигнал управления и и момент нагрузки Мс, действующий на ИО. Токовый контур замкнут через регулятор тока РТ. Блок ограничения БО предназначен для исключения возможности превышения якорным током двигателя предельно допустимого значения. В режиме Малых приращений передаточный коэффициент БО равен единице.

Даже при допущениях, связанных с представлением тиристорного преобразователя и датчика тока апериодическими звеньями н упрощенным описанием диссипативных сил, объект представляет