uJz)

Wjz)

и(2)

x(p)

Рис. 3.12. К возникновению ошибок второго типа

ветствующие им фазовые характеристики:

Фпо(«*) = ф1по (/©*)] = -(0.5 +т„*) to*". фп1 (со*) =ф (Wni (/со*)] = arctg (со*) -(I + т„,) со,.

Пусть некоторая нормированная частота сос, = ©сГо определяет область существенных частот для проектируемой системы, т. е. характеризует ее в отнощении необходимости воспроизведения во всей системе или ее отдельных частях самых быстрых изменений переменных. Тогда достаточно жестким условием возможности пренебрежения ошибками второго порядка можно считать фазовые искажения, вносимые Wno (/со*) или W„i (/со) на частоте Шс*, не превышающие одного градуса, т. е. выполнение условия фпо I < < 0,0175; фп1 < 0,0175.

На основании этих выражений на рис. 3.13 построены кривые, устанавливающие в интервале О < т„ < I соотношения между ©с* и Тм; при которых ошибками второго типа можно пренебречь. Сравнение кривых показывает, что применение ЦАП с характеристиками экстраполятора первого порядка значительно расширяет диапазон возможных соотношений между ©с* и Тм*, при которых ошибки второго типа не будут оказывать влияние на работу системы с ЭВМ в контуре регулирования. Аналогичного положительного результата можно добиться и при использовании экстраполятора нулевого порядка, если в прямой канал регулирования (рис. 3.12) ввести дополнительное корректирующее звено с передаточной функцией

(г)=.1

0,6г + 0,4

где Гк = 0,5 То + т„.

При такой компенсации ошибок второго типа возможность пренебрежения их влиянием может быть изучена на основе анализа частотных свойств последовательности звеньев

Wno(/4) «к(/Ч) = -

1 - е

1+(0,5+т„.)

0,6е-"Ч-0,4 (3.12)

0,10 0,08 0,0В

0,02 О

s)o,6

0,4 0,3 0,2 0,1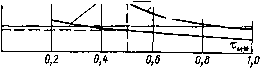

Зкстраполятор: нулевого порядка

первого порядка.

О 0,2 0,4 0,6 0,8 1,0

Рис. 3.13. К возможности пренебрежения ошибками второго типа

Для ЭТОГО на основании последнего выражения необходимо вычислить фазовые частотные характеристики фк = ф lUno X X {/©*) 1 при различных значениях т„ и определить такие соот- ношения между ©с* и Тм*, при которых выполняется неравенство <Рк! < 0,0175. Результаты такого расчета показаны на рис. 3.13, б.

Пусть в среднем на время вычисления алгоритма управления затрачивается половина периода дискретизации системы Т, т. е. выполняется условие Тм* = 0,5. Тогда из анализа кривых на рис. 3.13 следует, что ошибками второго типа можно пренебречь, если для ©с и информационной полосы частот дискретной системы ш„ = л/Го выполняются соотношения:

©с < 0,06©и или ©с < 0,013©и,

(3.13)

когда ЦАП имеет характеристику экстраполятора, соответственно, нулевого или первого порядка, и

©с < 0,11 ©и, (3.14)

когда в прямо.м канале управления применяется дополнительное корректирующее устройство.

Объект

a

Рис. 3.14. Структурная схема системы с наблюдателем при замене интеграторов их дискретной аппроксимацией

Выбор значения Го, при котором выполняется хотя бы условие (3.14), обеспечивает реализуемость алгоритма управления средствами ЭВМ на основе структурного метода.

В качестве примера обратимся к цифровой реализации непрерывной системы управления (см. рис. 3.2). Структурный метод предполагает формальный переход от аналоговой ДСС к описанию системы в дискретной форме. Результат такого перехода представлен в виде структурной схемы на рис. 3.14, где непрерывные процессы интегрирования заменены их дискретными аппроксимациями (3.7). В прямом канале управления учтено запаздывание на время вычисления алгоритма и преобразование сигнала из цифровой формы в дискретную, а в цепях обратных связей наблюдателя - запаздывание на время Т. На основании выполненной дискретной аппроксимации алгоритм управления может быть представлен в виде операторных уравнений:

«.1 (Z) = Ш1 (г) + 1гТГщ {г)~{кТ, ifx (г) г-\ хг (г) = (2) + (Го/Г,) [a„i (г) + (1 -(t„i) ui (г) г"»];

(г) -(2>+ 4Г„2\щ (г)- (z) 2-iJ; Xi (2) = 2i (2) + (Го/Гм2) [o„2U,2 (2) + (1 -Он) (z) г; и (2) = fejMy (z) - kiXx (2)-22 (г),