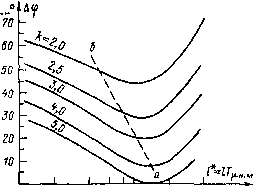0,1 0,2 0,4 1,0 2,0 4,0 Рис. 4.5. Зависимость запаса по фазе системы моделирования от параметров

И При замыкании контура по производной от скорости, если замедление при дифференцировании Характеризуется постоянной, численно равной времени Г.

Наличие контура моделирования Tui приводит к отличию передаточной функции Дц»! (р)/Дгя (р) от желаемой, которая должна представлять собой интегрирующее звено l/(T„ip). Вводя нормированную переменную р = Г„. „ р и обозначая т„.р = Гм.р/Тн. м, можно записать эту передаточную функцию в виде:

м. р

(1 + *) р.

Qip.y

(4.9)

где при принято.м описании токового контура

2р;+2(Г 1- 1)р + (2/* + \-k)p + С

Q,(p,) = (l+fe)-

2рЗ + 2 (Г + I) р2 + {21* +\)р -I- /• (1+;)

При /* <: {k-1)/2 частотная передаточная функция Q (/«*), где со* Гдн. м », становится неминимально-фазовой, что, как показывают расчеты, приводит к значительно.му искажению зависимости ю = / (гя) при скачке 1я. Это позволяет считать допустимыми значения /*, соответствующие части номограммы рис. 4.5, расположенной правее линии аб, отвечающей равенству /* = {k-\)l2.

Модель упругого механизма может быть выполнена как в аналоговой, так и в цифровой форме. На рис. 4.4,6 показана модель двухмассовой системы, в которой механическое демпфирование учтено коэффициентом kc- В соответствии с выражениями (2.2) при пренебрежении трением на массах можно записать передаточную

функцию, связывающую при управляющем воздействии упругий момент с током якоря:

д7я(Р) ту + к,тр+1

Формально эта функция, получается в результате замыкания единичной отрицательной обратной связью контура с выходной координатой М21 и передаточной функцией прямого канала

Wy(p}=----

Т.Г уту + kjp+i

При kc = О этот контур находится на границе устойчивости, благодаря чему в объекте существуют незатухающие колебания.

При полунатурном моделировании контур упругого момента реализуется с помощью связи по координате иу = модели механизма (рис. 4.4, б), вводимой на вход контура тока нагрузочной машины. Если показанная штриховыми линиями связь с коэффициентом aTfa.JTc отсутствует, то с учетом выражения (4.7) передаточная функция прямого канала контура упругого момента приобретает вид

Wy.Ap) = - .f"-Rip).

н. м (Р)

RiP)=

Тм.р 1 + «7/3. н. м (Р) k (1-р + 1-)*

Наличие сомножителя R (р), который в предположении о справедливости выражения (4.8) может быть переписан в виде

Rip)=.------- ,

при малых значениях kc приводит к отсутствию запаса по фазе и неустойчивости контура, моделирующего упругий момент. При постоянной времени Ту, хотя бы в четыре-пять раз превышающей значение Гн. м, фазовое искажение, вносимое этим сомножителем, может быть компенсировано введением форсирующего звена aTn.JT, реализующего производную от иу- Варьируя значение а, можно добиваться требуемого значения коэффициента kc.

Передаточная функция модели при управляющем воздействии в виде изменения тока якоря двигателя определяется в результате совместного решения (4.7) при Mci = О и второго и третьего уравнений системы (2.2) при АМц = Д«д,у и АМс = О- Рассматривая 154

наиболее тяжелый случай при /г = О и полагая в уравнении (4.7) «ВХ1 «му Н-а У" («1 -«шг) = «му(1 --аГ„. мр),

можно получить

Awi (р)

Ая (Р)

Гм. рР[Г/"з.„. „(Р) (-*Р + 1) + Н (v7yP>+ 1)+м2Р(Н-«Гц„.„р)(/-1р+1)

(4.10)

Полагая, что выполняется равенство (4.8), и вводя нормирование, как это сделано при записи формулы (4.9), можно передаточную функцию представить в виде

ДГя(р,) т„.р(1-/)р, tV+I

Sip,.), (4.11)

где Ту = Ту/7ун. м-

Сомножитель 5 (р) определяет отличие передаточной функции модели от желаемой. Вид частотной характеристики S Ца) зависит от Ту, у, k, аи I* (рис. 4.6). Сплошными линиями на рис. 4.6, а показаны ЛАЧХ для k = I при /* = 0,25, штриховыми - при /* = 0,75. Характеристики на рис. 4.6, б построены для /г = 3, причем сплошные линии относятся к случаю /* = 1, а штриховые - к /* = 3. Наличие при у > 1 «провала» характеристики на частоте 1/ту обусловливает демпфирование упругих колебаний при выбранном значении а. Резонансный «всплеск» при /г = 3 является результатом малого запаса по фазе при данном /* в соответствии с рис. 4.5.

Если для моделируемой АСУ ЭП зона существенных частот располагается вблизи частоты 1/Ту, то искажение характеристик АСУ ЭП за счет сомножителя S {\(л будет допустимым и установка полунатурного моделирования обеспечит нормальное функционирование испытуемой АСУ ЭП при Ту = 7у/7„. „>(4-5).

Сказанное иллюстрируется результатами эксперимента, приведенными на рис. 4.7. Установка полунатурного моделирования включала в себя две одинаковые машины ПБСТ-33 (1 кВт; 5,4 А; 220 В; 1000 об/мин). Тиристорные преобразователи ТП и ТПН ~ типа ПТЗР с согласованным совместным управлением. Наблюдатели и модель упругой системы выполнены на операционных усилителях, регуляторы тока и скорости исследуемой системы - на элементах УБСР. Малые постоянная времени и реальная механическая постоянная времени стали равны Ti = Tа,ы = 0,02 с;