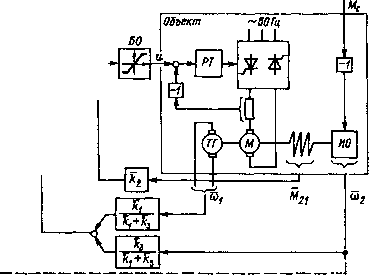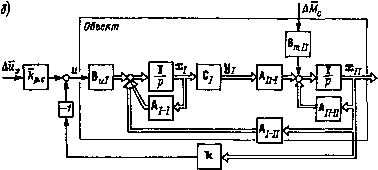Рис. 2.10. Система управления скоростью, замкнутая по вектору состояния механизма: а - функциональная схема; б - матричная структурная схема

собой достаточно сложную динамическую систему. Порядок системы увеличивается, если существует замедление, вносимое датчиками, установка которых предполагается для измерения со, М21 и (Л2- Очевидно, что сколько-нибудь общие выводы о свойствах рассматриваемой АСУ ЭП могут быть получены только при разумном упрощении ее математического описания. В дальнейшем в настоящей главе рассмотрение ведется при следующих допущениях:

1. Система линеаризована, что предполагает, с одной стороны, пренебрежимо малое влияние зазоров и нелинейного трения, а с другой,- такие значения внешних воздействий, при отработке которых якорный ток не превышает предельно допустимого значения и система токоограничения не действует.

2. Сформулированные в § 2.2 условия пренебрежения обратной связью по ЭДС двигателя выполняются, и настроенный на оптимум по модулю токовый контур приближенно описывается передаточной функцией

(2.16)

где Тцэ == 2Гд/ - эквивалентная малая постоянная времени.

3. Датчики скорости и упругого момента представляют собой пропорциональные звенья, благодаря чему при рассмотрении математического описания системы в относительных единицах можно считать, что связи с коэффициентами fej, feg и feg выполнены непосредственно по «1, Мгхисог. Если же быстродействие датчиков ограничено, то, считая, что оно характеризуется одинаковой постоянной времени Тф, можно принять Тэ = 2Т,-{-Тф.

4. Силы трения не учитываются, т. е. принимается kfi - kf = = ft, = 0.

Записывая матричное уравнение объекта в виде

х-Ах-ЬВ„«+В„ДМс,

(2.17)

можно построить матричную структурную схему системы (рис. 2.10, б). Вектор состояния объекта разделен на вектор х, = = col IxiXl, элементами которого являются координаты токового •контура при = Ai„, и вектор состояния механизма хц =

= col [XgXiXj] при Хз = Acoj; Х4 = АМ21; Х5 = Acoj. С помощью матрицы Ci из XI выделяется вектор уь в конкретном случае представляющий собой координату Xg = г/ь Тогда

L т

2 1

цэ

; Ai ii = 0; B„i =

АМс. (2.18)

Аа [ =

г 1 п

Ci = lO 1];

Ап п

mil -

Тс О

Тш О

Статическая система. Если регулятор скорости пропорциональный (показанный на рис. 2.10, а штриховыми линиями канал введения интеграла в закон регулирования отсутствует), система будет иметь статическую ошибку по возмущению. При отсутствии возмущения выбор ftp.с = fei 4-3 обеспечивает равенство установившихся приращений Acoi уст = Асог уст = А"у-

В замкнутой системе управление записывается как

u=fep. сА«у-кхп,

где к = [kikik]. Тогда с учетом введенных в § 2.1 обозначений могут быть записаны передаточные функции, связывающие приращения скоростей Acoj и Асог с приращением управляющего воздействия Аыу:

. г„1з (р) = (Р)/Д«у (Р) = {ут\р+т (Р);

Гс,2з(р) = А«2(р)/А«у(р) = 1/С(р).

Здесь

(2.19)

Q{p) =

ы \1э

Н{Р)

(2.20)

р. с

Я(р) = с1е1(р1-А~В„к) = р* + -Р* +

( П )

цэ м

цэ у

г2 тт

цэу н