Авсв

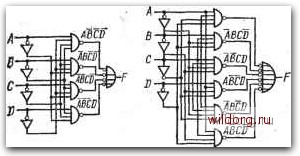FABCB+ABCD+fiBCBtfiBCB

. a)

В=Ж1]+АВСВНВСВ+АбФ

, В) .

F=ABj:V+ACB+ABCSi-ABS ч-АВСВч-АВСВ

Рис. 5.30. a) Детектор 1 из 4; б) детектор 2 из 4; в) детектор 3 из 4

ВОЙ цепи 2 из 10. Принцип заключается в том, что входные переменные, например, 1, 2, 3- объединенные одной, суммирующей цепью, далее должны быть подключены к различным суммирующим цепям. Таким образом, возникает избыточность, так как комбинации некоторых входных переменных появляются несколько раз, но составление схемы очень просто. На рис. 5.316 - такая

И-НЕ И-НЕ И-НЕ

И-НЕ

Рис. 5.31. а) Пороговая цепь 2 из 10; б) уирощеиная схема « использованием логи-i Кй на объединенных выходах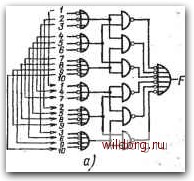

4>

же схема с использованием логики на объединенных входах.

Составление цепи с порогом 3 для любого числа четных входов тоже несложно. Обозначим для наглядности входы цифрами 1, 2, 3, п, тогда выходная функция пороговой цепи F{3 из п)=1-2-(3+4+5+...+п)-Ь3.4.(1+2+5+6+7+8+...+п)+ -f 5-6-(H-2+3+4+7-f8+9+10-f...-fn)+... + [l+2-f3-f4+... + (n-2)]+f[3 из (1+2), (3+4),

(5+6)...., (п+-2-1)1. (5.3)

1 .125

h-5.

Например, для пороговой цепи 3 из 10 справедливо

f (3 из 10)=1-2-(3+4+5+6+7+8+9+10) +

+3 •4-(1 + 2+54-6+7+8+9+10)+

+ 5-6-(1+2+3+4+7+8+9+10)+7.8 .(1+2+3+4+

+ 5+6+9+10)+9 • 10 -(1 +2+3+4+5+6+7+8)+

. +F[3h3 (1+2), (3+4). (5+6), (7+8), (9+10)].

Соответствующую схему см. на рис. 5.32: пороговую цепь 3 из 5 можно составить так, как это описывалось в начале главы. Пороговую цепь 3 из п для нечет--1 ного числа входов можно составить так же, как в случае четного числа входов, а нечетный вход подключить к дополнительному конъюнктору на выходе схемы. Например, для цепи 3 из 11 используется схема на рис. 5.32, выход р (3 из 10) который объединяется: с нечетным, одиннадцатым входом с помощью конъюнктора.

Рассмотренные пороговые цепи, проектируемые в базисе типовых логических схем, сравнительно сложны и требуют большого числа базовых логических элементов. Их реализация выгодна только при использовании интегральных схем, и тогда нет проблем свя-

Щ-Г{3из10)

Рис. 5.32. Пороговая цепь 3 из 10

занных с допусками на параметры элементов и напряжения питания. Вместо этих сложных схем могут быть использованы очень простые пороговые цепи с резистивной, диодной или эмиттерной связью, основные схемы которых были представлены в § 1.10 в связи с мажоритарными цепями. Эти цепи характеризуются минимальным числом элементов, однако для них большое значение имеет отклонение параметров отдельных элементов и напряжения питания.

5.8. СУММИРУЮЩИЕ И ВЫЧИТАЮШДЕ УСТРОЙСТВА Типы сумматоров

Сложение в двоичной системе счисления является самой важной арифметической операцией, так как оно лежит в основе других арифметических операций: вычитания, умножения, деления. Основными схемами, обеспечивающими элементарные операции сложения, являются так называемые одноразрядные сумматоры.

которые могут быть полными и неполными. Неполный сумматор имеет только два входа и два выхода. Один выход дает результат сложения двух бит, а второй выход дает результат переноса, возникающего при сложении, т. е. неполный сумматор представляет собой, в принципе, элемент ИСКЛЮЧАЮЩЕЕ ИЛИ, дополненный выходом переноса.

Полный одноразрядный сумматор имеет три входа и два выхода. На третий вход подается результат переноса предыдущего сумматора. Большое значение имеют полные одноразрядные сумматоры, которые можно составить из двух неполных. Суммирование большего числа бит может быть последовательное или параллельное. В последовательных сумматорах отдельные биты обрабатываются последовательно, начиная с младшего разря.ца; для записи переносов, возникающих при сложении младших разрядов, необходимы тригерры. Их принцип действия будет объяснен ниже. В параллельных сумматорах все биты обрабатываются одновременно, сложение производится быстрее, но схемы более сложные. В связи с тем, что сумматоры широко используются, они выпускаются как полностью интегральные схемы. Различные примеры применения таких сумматоров будут приведены далее.

Одноразрядные неполные сумматоры

Комбинационная таблица неполного сумматора -представлена на рис. 5.33. В принципе это схема ИСКЛЮЧАЮЩЕЕ ИЛИ, дополненная выходом С, который имеет значение 1 только тогда, когда одновременно на обоих выходах ~ А и В - имеется 1.

Рис. 5.33. Неполный одноразрядный сумматор:

а) комбинационная таблица; б) схема в базисе И-НЕ и условное обозначение

S=AB-t-AB С=АВ

--Сумма

I- Перенос

-4> 6)

-S -С

Пример такой схемы в базисе И-НЕ показан на рис. 5.336. В ка-, честве базовых элементов одноразрядных неполных сумматоров могут быть использованы элементы, представленные в табл. 5.1. Из непол.ных сумматоров могут быть составлены полные, которые находят применение во всех случаях, когда, кроме функции исключающего логического сложения ИСКЛЮЧАЮЩЕЕ ИЛИ