Предполагается, что задержки одинаковы, но в реальной схеме они неодинаковы. Характер изменения Yi и Y2, конечно, вымыш-

ленный.

Рис. 6.9. JS-триггер типа ИЛИ-НЕ:

а) карта и диаграмма переходов для нормальных рабочих условий;

б) временная диаграмма

i i i i

1 i

►it

Синтез RS-триггера типа ИЛИ-НЕ. При синтезе исходят из словесной формулировки заданной проблемы или из временной диаграммы. Требуемую функцию основного триггера представляет временная диаграмма на рис. 6.10а, на которой последовательно отмечаются все устойчивые состояния. Для большей наглядности на рис. 6.106 показаны также временные зависимости, которые могут иметь место в реальной схеме, причем на них обозначены и неустойчивые состояния. Однако для синтеза схемы достаточно временной диаграммы, на которой отмечены только устойчивые состояния.

На основе рис. 6.10а составляется примитивная таблица развития. Процесс ясен из рис. 6.11а. Устойчивые состояния обозначаются кружком, неспецифицированные состояния - черточкой. В каждой строке есть только одно устойчивое состояние, каждой строке соответствует определенное состояние выходов Qi и Qz.

Количество строк в таблице нужно уменьшить до минимума, так как обычно таблица содержит больше устойчивых состояний, чем это нужно в действительности. Преобразование таблицы основано.

0 -I

1

О®

о 1

(7) 2 ®3Q)Z®3(3) 4®1Ф(.®1Ф

Рис. 6.10. а) Упрощенная временная диаграмма требуемой функции iRiS-тригге-ра типа ИЛИ-НЕ; б) реальные временные зависимости с обозначением неустойчивых состояний без кружков

во-первых, на определении избыточных устойчивых состояний, а во-вторых, на соответствующем объединении строк. Два устойчивых состояния в одном столбце таблицы тождественны, если им соответствуют одинаковые состояния выходов и одинаковые или эквивалентные неустойчивые состояния других столбцов. Ясно, что в простой таблице на рис. 6.11а избыточных состояний нет.

00 01 11 10

ж ® ©

10 б)

M,F+SR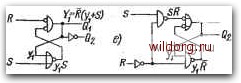

Puc. 6.11. a) Примитивная таблица развития, составленная по рис. 6.10; б) диаграмма объединения; е) сокращенная таблица развития; е) карта развития, карта функции У и ее определение, карты переходов; д) триггер на базовых элементах ИЛИ-НЕ; е) на элементах И-НЕ

Редукцию таблицы обеспечит объединение соответствующих строк. Обычно можно объединять строки без учета состояния выходов Qi, Qz, если количество устойчивых и неустойчивых состояний в соответствующих столбцах соответствующих строк одинаково. При этом неустойчивое состояние заменяется устойчивым, а неопределенное состояние (горизонтальная черточка) - устойчивым или неустойчивым. Большую помощь при этом оказывает диаграмма объединения на рис. б.Пб, которая для рассматриваемого примера очень проста, но в более сложных случаях наглядно показывает все возможности объединения строк примитивной таблицы развития. Объединяют по возможности строки с одинаковым состоянием выходов. При объединении строк, соответствующих неодинаковым состояниям выходов, появляется необходимость подключения к ним комбинационной логической схемы. Объединяя строки а, d я Ь, с, получаем сокращенную таблицу развития (рис. 6.11в)..

Эта таблица имеет только две строки, йз чего следует, что результирующая схема может иметь только одну петлю обратной связи, т. е. только одну внутреннюю переменную tji с двумя состояниями- О и 1. Сокращенную таблицу переводят в карту развития на рис. 6.11г и переменной придают значения 1 и О таким образом, чтобы они соответствовали значениям Qi надлежащих строк. По карте развития составляется карта функции Yi. В поле, которому соответствует устойчивое состояние, должно быть 1=1; в поле с неустойчивым состоянием должно быть выполнено условие Yiyi. Неопределенные состояния, обозначенные горизонтальной черточкой, не имеют значения с точки зрения требуемой функции, поэтому им могут соответствовать значения Yi как О, так и 1. Объединяя поле со значением 1, получают алгебраическое выражение функции Yi в форме дизъюнкции конъюнкций. На рис: 6.115 показан пример реализации триггера на элементах ИЛИ-НЕ, на рис. б.Пе - на элементах И-НЕ. Выход Qi=yi, дополняющий выход Q2, получается с помощью инвертора.

Рис. 6.12. Возможность получения других схем триггера

Yi=yiR+SR

Y]=y,R-i-S

Yi=y,R+SR+jiS

Yi=y,R*SR+yiS

Кроме схемы на рис. 6.11, может существовать еще много других в зависимости от того, какие значения, О или 1, будут соответствовать неспецифицированным состояниям в столбце Si? = 11. Эти различные варианты показаны на рис. 6.12. Все схемы, получен-