записывается только в карты функций F2 и fs- Наконец, определяем произведения, входящие в отдельные функции. Это произведения: АС в Fu АВ ъ Fz АВ в "3. На рис. 4.166 представлена результирующая схема на элементах И-НЕ.

В этом случае требуется восемь схем И-НЕ, четыре из которых должны иметь три входа и четыре - два входа. В обычном корпусе с 14 выводами размещены четыре интегральные схемы И-НЕ с двумя входами или три интегральные схемы с тремя входами. Таким образом, для реализации необходимы один корпус с двухвходовыми схемами и Р/з корпуса с трехвходовыми схемами. Необъединенные минимизированные основные функции имеют вид

Fi=AB+AC, F=AC+BC+AB, РАВ+АС+ВС.

Для реализации схемы при этом необходимо 274 корпуса с двухвходовыми схемами и 2/3 корпуса со схемами с тремя входами. Экономится примерно 2/3 корпуса. При использовании более дешевых интегральных схем целесообразно заранее решить, будет ли достигнутая экономия уравновешена временем, потраченным на объединение групп более сложных схем. Это относится прежде всего к проектированию прототипов цифровых систем.

ГЛАВА 5

Комбинационные логичеекие схемы

5.1. ПОСЛЕДОВАТЕЛЬНОСТЬ СИНТЕЗА

У комбинационных логических схем состояние выхода зависит только от состояния их входов в данный момент. Систематический анализ и синтез этих схем можно осуществить методами, рассмотренными в предыдущих главах. При проектировании комбинационных схем целесообразно придерживаться следующей последовательности:

а) логическое утверждение данной проблемь! выражается комбинационной (истинностной) таблицей со всеми возможными комбинациями входных переменных и с требуемыми выходами для каждой комбинации входных переменных;

б) с помощью карт Карно или других методов определяются минимизированные выражения результирующих логических функций;

в) в соответствии с предполагаемыми для использования схемами алгебраические выражения преобразуются в логическую схему.

Такой систематический процесс обеспечивает правильную функцию результирующих логических схем, потому что рассматриваются все возможные комбинации, а результирующие схемы являются оптимальными, так как в процессе решения исключаются ненужные комбинации, которые на первый взгляд могут показаться требуемыми. Ниже приводятся некоторые типичные примеры составления комбинационных схем, часто используемых в полупроводниковых цифровых системах. В большинстве случаев это параллельные схемы, обрабатывающие все биты одновременно. Рассматриваются только основные схемы - И, ИЛИ, И-НЕ, ИЛИ-НЕ - в положительной логике.

5.2. ОСНОВНЫЕ СХЕМЫ, ПРЕДНАЗНАЧЕННЫЕ ДЛЯ ОПРЕДЕЛЕНИЯ РАВНОЗНАЧНОСТИ

И НЕРАВНОЗНАЧНОСТИ ВХОДНЫХ ПЕРЕМЕННЫХ

Принцип этих схем основан на логической функции ИСКЛЮЧАЮЩЕЕ ИЛИ. При наличии двух входных переменных - An В - эта функция определена основным соотношением

F=A®B=AB+AB=(А+В) {А+Щ. (5-1

4* 89

Важным свойством этой основной функции является то, что она имеет значение F= 1 только тогда, когда значение 1 имеет только одна входная переменная, а вторая переменная имеет значение О, т. е. определяет неравнозначность входных переменных А vl В. Следующая основная функция:

Р=А®В=АВ+АВ=(А+Щ(А+В). (5.2)

Эта функция, наоборот, имеет значение 1 только тогда, когда обе

Таблица 5.1. Примеры логических схем

-ав-ав

в -Л

-АВ*АВ

А-\\АЗ

А - В -

ав*ав

в -и\ шв

В

А-В-

,а*в

ВХА*ВУ в*ав

а -в-

а-в-

~1-ГХАу)==

[А*В)(МВ}= Ш+АВ

..TUBtAB J%B

А -ГЖ

в -1/~Цч-Л5=

-ТаШв

ав*ав

Ма4)АВ

ав*ав

МАВ=Мд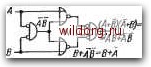

I Uj

МААВ

/в{а*внв

-1-:-\)в{А*ВУ=АВ

4j