!3 6 С S

1010 +0011

01101

A В Ci CdS S

A в Ci CdS S

A В

С S

A3B3

1 1 A2B2

A в Ci CpS s

A в Ci

Ci=0

A В Ci CoS S

82=0 Sri

AiBi

A В d CqSS

S.i=1

SzO Sri

Puc. 5.40. Параллельный четырехразрядный сумматор: a) составленный из неполных одноразрядных сумматоров; б) из полных сумматоров с совпадающими логиче-скими полярностями переносов С{ и Cq; е) из дуальных сумматоров

1 О А,, В,,

О О 13 Вз

О 1 1 Bi

ABC, CoSS

-Cri

A В Ci CdS 5

B--0 D3-I

Ai,B,, ABj A2B2 4Bj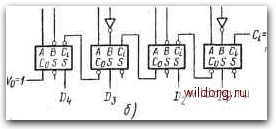

Единичное дополнение

Ддоичнов дополнение

А =1010 В 0011 в =1100

1100 + 1

1010 +1101

Jlll =Ад

Ч 1101

в сумматоре

младшего разряда

Рис. 5.41. Вычитание двоичных чисел: а) с помощью одно1разрядных сумматоров с совпадающей логической полярностью переноса; б) с помощью дуальных сумматоров

и прибавления к Bi единицы. Это прибавление реализуется тем, что вход Сг сумматора младшего разряда имеет постоянное значение 1. Если С4=1, то результирующая разность будет положительным числом (А>В), если же С4=О, то разность - отрицательное число (A<iB). На рис. 5.416 использованы дуальные сумматоры. В отличие от дуальных сумматоров на рис. 5.4,0в здесь не использованы внутренние инверторы, включенные последовательно входам В. обозначенным кружками. Этим входам соответствуют, например, входы В1В2 сумматора на рис. 5.37а hjjh прямые входы А, В сумматора на рис. 5.37в.

Ускорение переноса при сложении двоичных чисел

Из представленных выше примеров схем вытекает, что переносы С последовательно проходят между отдельными сумматорами от самого младшего до самого старшего разряда. Результирующая сумма появляется на соответствующих выходах 5 только после обработки переноса, поступившего в сумматор самого старшего разряда. Это так называемые параллельные п-разрядные сумматоры с последовательным переносом. Ускорение операции сложения обеспечивает параллельный перенос, который можно реализовать, пользуясь соответствующими преобразованиями основных алгебраических соотношений, выражающих функцию передачи. Предположим, например, согласно (5.6) у сумматора п-го разряда

С=АВ+{А+В)Сп-х. (5.14)

Бели Л = 0 и В = 0, то обязательно и С=0. Перенос Сп = 1 только тогда, когда одновременно А = 1, В = 1, или А1, Cn-i = l, или В=1, Сп 1=1. С точки зрения возникновения переноса 1 будем далее рассматривать так называемую образующую (генерирующую) функцию G = AB, имеющую значение 1 только в случае, если А=1 и В = 1. Если у п-го сумматора G„=l, то перенос будет иметь место именно в этом сумматоре. Другая, так называемая функция переноса Р=А + В имеет значение 1, если Л=1 или В = - I. Если у сумматора разряда п значение Р-1, то перенос G„ i = l передается сумматору разряда п+1. Соотношение (5.14) имеет теперь вид С„= Gn+PnCn-i. Для рааряда п-1 аналогично C„ i = G„ i-f Pn-iC„ 2. Подставив C„ i в первую формулу, получаем C„ = G„ + P„G„-i-fPnPn-iC„ 2 и т. д. Итерация основного соотношения позволяет получить формулу переноса п-го разряда

Cn=G+PnGn-i+PnPn-iGn-2+:..+PnPn-iPn-2-PGo. (5.15)

Перенос, представленный в таком виде, позволяет создать более быстродействующие сумматоры, так как значение переноса зависит не от предыдущего переноса, а от значений генерирующих функций -и функций переноса.

Для нагладности на рис. 5.42 показана схема многоразрядного сумматора на базовых элементах И и ИЛИ. Ясно, что с увеличением числа суммируемых разрядов увеличиваются и требования,

Ускорение переноса

J-T-% г1-<

- Й2

2 «2

Рггс. 5.42. Четырехразрядный сумматор с ускорением переноса

предьявляемые к числу входов базовых элементов. Рассмотрим, например, реализацию ускоряющих цепей четырехразрядного сумматора на базовых элементах И-НЕ, пользуясь алгебраическим выражением переноса в виде

C„=G„+P„C„ .=AA-f0A+4fi„)C„ .. (5.16)

Согласно (5.15) справедливо

C=G+Pfi+PJG+PPPfi+PJPJ>fi„ (5.17)

Go = Ci - перенос в сумматор младшего разряда.

Двукратным использованием закона де Моргана преобразуем соотношение (5.17) таким образом

C=GJ>+Gfi+GGfiP+GfifiGj+

аналогично

+GfiGGCfiJ>=AB{Afi+AB)=A+B,

СзРз=4+£з. ОаРа+Л+г. GJ>=A+B,

СА=е4+Сз=4В,+4Вз, GG=G+G=A+AB.